Acronym ML stands for maximum likelihood.
ML estimators are calculated in such a way that they maximize the likelihood of n independent observations. That is, if \(f(x_i; \theta_1, \ldots, \theta_p)\) is the value of the density function for the i-th observation, which depends on parameters \(\theta_1, \ldots, \theta_p\), the function to be maximized is \[ L(\theta_1, \ldots, \theta_p; x_1, \ldots, x_n) = \prod_{i=1}^n f(x_i; \theta_1, \ldots, \theta_p). \] The set of numbers \(\hat{\theta}_1, \ldots, \hat{\theta}_p\), such that they maximize \(L\), are the so called maximum likelihood estimators.
First, we load package distrib,
load("distrib")$
Given a normal, or gaussian, population with unknown parameters \(\mu\) and \(\sigma\), once we have an independent sample of size n, \((x_1, x_2, \ldots, x_n)\), our likelihood function takes the form
L: product(pdf_normal(x[i],mu,sigma), i, 1, n);
\[ \prod_{i=1}^{n}{{{e^ {- {{\left(x_{i}-\mu\right)^2}\over{2\,\sigma^ 2}} }}\over{\sqrt{2}\,\sqrt{\pi}\,\sigma}}} \]
Taking the logarithm of the above expression, we get the loglikelihood function,
logL: ev(log(L), logexpand=all);
\[ \sum_{i=1}^{n}{\left(-\log \sigma-{{\left(x_{i}-\mu\right)^2}\over{ 2\,\sigma^2}}-{{\log \pi}\over{2}}-{{\log 2}\over{2}}\right)} \]
As we want to maximize the likelihood, or equivalently the loglikelihood, we need to equal to zero the partial derivatives of the loglikelihood with respect to \(\mu\) and \(\sigma\). The derivative with respect to \(\mu\) is
logLmu: ev(diff(logL, mu), simpsum=true);
\[ {{\sum_{i=1}^{n}{x_{i}}-\mu\,n}\over{\sigma^2}} \]
Equating to zero and isolating \(\mu\) yields
hatmu: solve(logLmu, mu);
\[ \left[ \mu={{\sum_{i=1}^{n}{x_{i}}}\over{n}} \right] \]
Which we recognize as the sample mean, so that our result can be summarized as \(\hat{\mu}=\bar{x}\).
We repeat a similar procedure for \(\sigma^2\),
logLsi: ev(diff(logL, sigma), simpsum=true) $ hatsi: solve(logLsi, sigma^2);
\[ \left[ \sigma^2={{\sum_{i=1}^{n}{\left(x_{i}-\mu\right)^2}}\over{n }} \right] \]
Which is the sample variance, so that \(\hat{\sigma}^2=s^2\).
The expression for the variance can be written only in terms of the sample values,
subst(hatmu, hatsi);
\[ \left[ \sigma^2={{\sum_{i=1}^{n}{\left(x_{i}-{{\sum_{i=1}^{n}{x_{i} }}\over{n}}\right)^2}}\over{n}} \right] \]
Let us now proceed with the numerical part of this session. Instead of taking our sample from a real world population, we can make a simulation calling function random_normal from package distrib. Let \(n=50\) be the sample size, \(\mu=50\), and \(\sigma=2.5\),
(n: 50, mu: 50, sigma: 2.5) $ fpprintprec: 4 $ x: random_normal(mu, sigma, n) ;
\[ \left[ 53.21 , 50.45 , 52.16 , 51.37 , 44.37 , 52.65 , 50.92 , 51.25 , 52.18 , 48.49 , \\ 52.49 , 46.19 , 47.32 , 47.73 , 50.58 , 48.6 , 49.21 , 52.32 , 49.95 , 48.7 , \\ 55.38 , 51.36 , 48.3 , 49.34 , 52.6 , 48.8 , 47.52 , 44.53 , 49.25 , 44.47 , \\ 48.58 , 48.33 , 48.39 , 49.36 , 43.98 , 53.73 , 51.93 , 51.76 , 46.22 , 53.61 , \\ 51.2 , 50.16 , 54.3 , 46.86 , 56.86 , 49.21 , 50.75 , 45.22 , 53.87 , 48.85 \right] \]
In order to calculate the sample mean and variance, we need to load the descriptive package. We also include the sample standard deviation,
load("descriptive") $
ml: [mean(x), var(x), std(x)];
\[ \left[ 49.9 , 8.529 , 2.92 \right] \]
As a result, \(\hat{\mu}=49.9\), and \(\hat{\sigma}=2.92\). Remember that our sample was artificially drawn from a normal population with parametrrs \(\mu=50\), and \(\sigma=2.5\). Also remember that the ML estimator of the variance is a biased estimator.
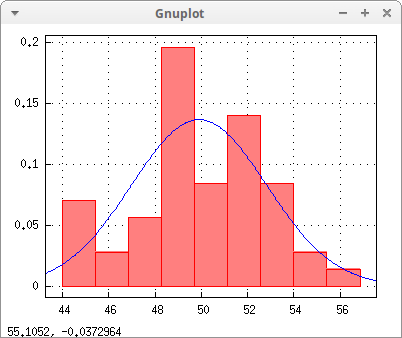
With help of function histogram, also implemented in package descriptive, we can show a graphical representation of the sample together with the estimated gaussian probability density,
[m, s]: [ml[1], ml[3]] $
draw2d(
grid = true,
dimensions = [400,300],
histogram_description(
x,
nclasses = 9,
frequency = density,
fill_density = 0.5),
explicit(pdf_normal(z,m,s), z, m - 3*s, m + 3* s) ) $
© 2017, TecnoStats.