Back to draw-Gnuplot

Affine transformations

In case of affine transformations, it's easier to work directly with matrices. First, we need a function to transform a matrix into the required syntax of option transform:

matrix_to_transform_format (m,[vars]) :=
  block([prod, lv: length(vars)],
   if not member(lv, [2,3]) or
      not every (atom, vars) or
      not matrixp(m) or
      length(m) # length(first (m)) or
      length(m) # lv + 1
     then error("Illegal definition of variables")
     else prod : m . transpose(endcons(1,vars)),
          append(makelist(prod[k,1], k, 1, lv),
                 vars) )$

Let's now define some affine 2D transformation matrices:

/* Rotation of angle th */
rotation(th) := matrix([cos(th),-sin(th),0],[sin(th),cos(th),0],[0,0,1])$

/* Scaling with factors k1 and k2 */
scale(k1,k2) := matrix([k1,0,0],[0,k2,0],[0,0,1])$

/* Translation with respect to vector (u,v) */
translation(u,v) := matrix([1,0,u],[0,1,v],[0,0,1]) $

/* Reflection through x-axis */
reflection_x() := matrix([1,0,0],[0,-1,0],[0,0,1])$

/* Reflection through y-axis */
reflection_y() := matrix([-1,0,0],[0,1,0],[0,0,1])$

/* Reflection through the straight line which passes 
   through point (p1,p2) with direction vector (u1,u2) */
reflection_line(u1,u2,p1,p2) :=
    block([th:atan2(u2,u1)],
        translation(p1,p2) .
        rotation(th) .
        reflection_x() .
        rotation(-th) .
        translation(-p1,-p2)) $

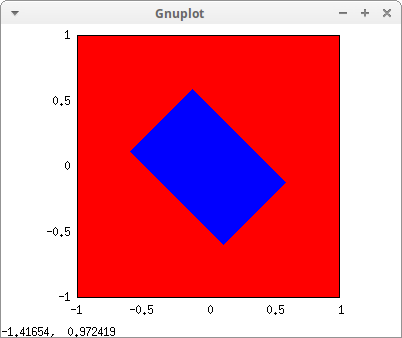
Scaling and rotating a square:

quad : rectangle([1,1],[-1,-1]) $
draw2d(
   proportional_axes = 'xy,
   /* original red square */
   quad,
   transform         = matrix_to_transform_format (
                            rotation(%pi/4) . scale(1/3, 1/2),x,y),
   fill_color        = blue,
   /* transformed blue rectangle */
   quad ) $

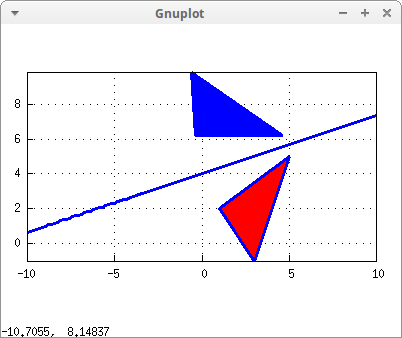
Reflecting a triangle through an arbitrary axis:

tri : triangle([1,2], [5,5], [3,-1]) $

/* the symmetry axis is the straight line with director vector
   (3,1) passing through point (0,4), whose equation is y = 4 + x/3 */
draw2d(
   proportional_axes = xy,
   line_width       = 3,
   grid             = true,
   tri,
   explicit(4 + x/3,x,-10,10),
   transform        = matrix_to_transform_format (reflection_line(3,1,0,4),u,v),
   tri )$

An example in 3D. Rotating a cylinder around an arbitrary axis:

/* Rotation of angle th around axis passing through point p=[p1,p2,p3]
   with direction vector u=[u1,u2,u3] */
rotation3d(th,u,p) :=
  block([c,s,t,n],
    c : cos(th),
    s : sin(th),
    t : 1 - c,
    n : u / sqrt(apply("+", u^2)),
    matrix(
      [t*n[1]^2+c,         t*n[1]*n[2]-s*n[3], t*n[1]*n[3]+s*n[2], p[1] ],
      [t*n[1]*n[2]+s*n[3], t*n[2]^2+c,         t*n[2]*n[3]-s*n[1], p[2] ],
      [t*n[1]*n[3]-s*n[2], t*n[2]*n[3]+s*n[1], t*n[3]^2+c,         p[3] ],
      [0, 0, 0, 1] ))$

set_draw_defaults(
  xrange = [-5,5], xlabel = "x",
  yrange = [-5,5], ylabel = "y",
  zrange = [-5,5], zlabel = "z",
  proportional_axes = xyz,
  xyplane           = 0,
  points_joined     = true) $

/* graphic objects */
cylinder : tube(0,3,a,1,a,-2,2) $
rotation_axis : points([[0,1,4],[0,-1,-4]]) $
rotated_cylinders :
    makelist(
          gr3d(
              view = [60,5*k], /* we also rotate our point of view */
              rotation_axis,
              cylinder,   /* original cylinder */
              transform  = matrix_to_transform_format(
                               rotation3d(k*2*%pi/15,[0,1,4],[0,0,0]), x,y,z),
              color      = red,
              enhanced3d = true,
              cylinder),
          k,0,15) $

draw(
 dimensions = [400,400],
 delay      = 20,
 terminal   = animated_gif,
 rotated_cylinders )$

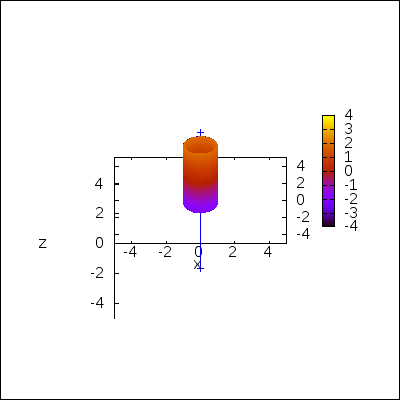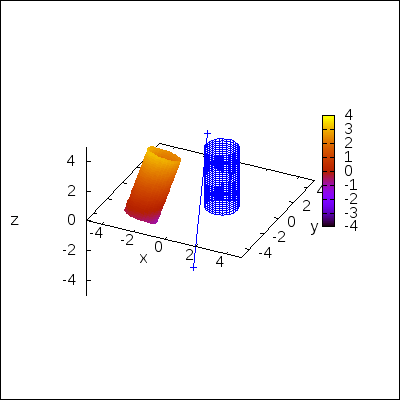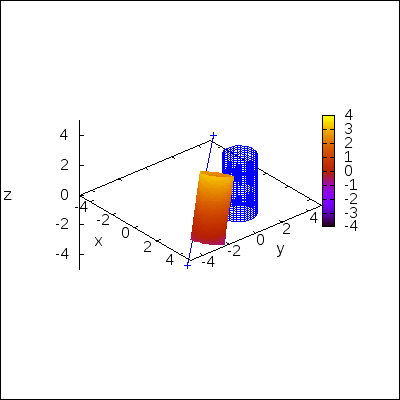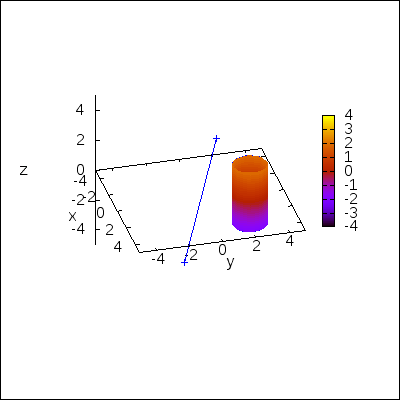
© 2011-2016, TecnoStats.