Back to draw-Gnuplot

'draw'-Gnuplot interface:
object implicit

• Implicit functions in R²
• Implicit functions in R³

Once you have opened a Maxima session, load package draw:

load("draw") $

To read the documentation on object implicit, write the following sentence:

describe(implicit) $

Implicit functions in R²

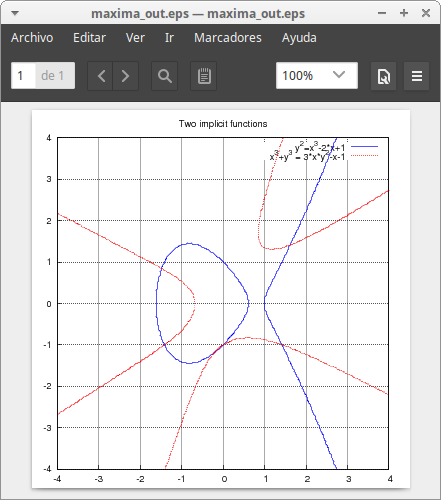
Two implicit functions in 2d:

draw2d(
  terminal   = eps_color,
  dimensions = 100*[10,10],
  grid       = true,
  line_type  = solid,
  key        = "y^2=x^3-2*x+1",
  implicit(y^2=x^3-2*x+1, x, -4,4, y, -4,4),
  line_type  = dots,
  color      = red,
  key        = "x^3+y^3 = 3*x*y^2-x-1",
  implicit(x^3+y^3 = 3*x*y^2-x-1, x, -4,4, y, -4,4),
  title      = "Two implicit functions" ) $

Implicit functions in R³

Gnuplot is not the best tool for 3d modelling tasks, but with some tricks we can get implicit surfaces. The method used by Maxima is the marching cubes triangularization algorithm.

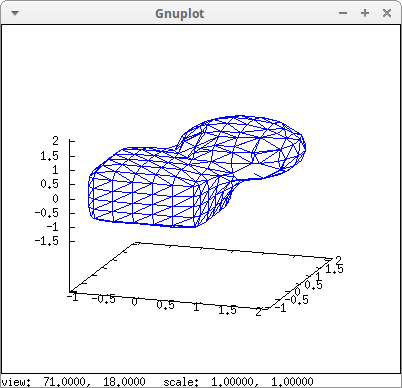
Union of two 3d objects:

draw3d(
  implicit(min((x-1)^2+(y-1)^2+(z-1)^2, x^6+y^6+z^6)=1,
           x,-1.1,2.1,y,-1.1,2.1,z,-1.5,2.1),
  surface_hide = true)$

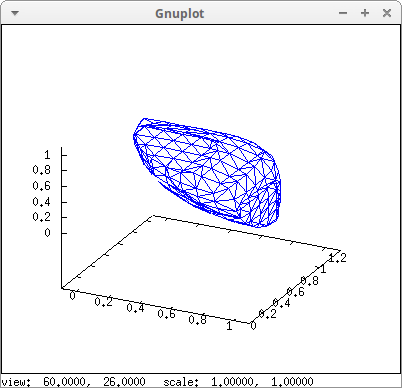
Intersection of the same objects:

draw3d(
  implicit(max((x-1)^2+(y-1)^2+(z-1)^2, x^6+y^6+z^6)=1,
           x,-0.1,1.1,y,0,1.3,z,-0.1,1.1),
  surface_hide = true)$

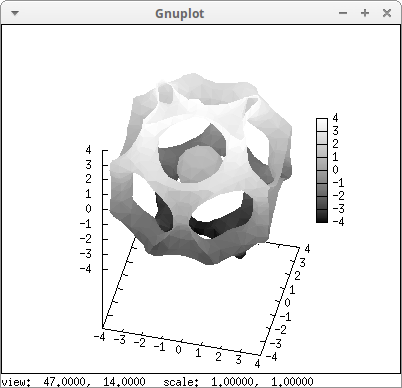
Icosahedral symmetry. %phi is the golden ratio:

draw3d(
  proportional_axes = xyz,
  enhanced3d        = true,
  x_voxel           = 15,
  y_voxel           = 15,
  z_voxel           = 15,
  implicit(2=(cos(x+%phi*y)+cos(x-%phi*y)+cos(y+%phi*z)+
             cos(y-%phi*z)+cos(z-%phi*x)+cos(z+%phi*x)),
           x,-4,4,y,-4,4,z,-4,4),
  palette           = gray,
  surface_hide      = true)$

Some more examples, suggested to me by Wolfgang Lindner. We see here how different look the same surfaces plotted by different draw graphics objects: implicit vs spherical and cylindrical; the resulting triangles are evident in the first case:

scn1: gr3d(
  color        = red,
  implicit(x^2+y^2+z^2=1,x,-1.5,1.5,y,-1.5,1.5,z,-1.5,1.5),
  color        = green,
  implicit(2*x^2+2*y^2=1,x,-1.5,1.5,y,-1.5,1.5,z,-1.5,1.5),
  surface_hide = true)$

scn2: gr3d(
  color        = red,
  spherical(1,a,0,2*%pi,z,0,%pi),
  color        = green,
  cylindrical(1/sqrt(2),z,-1.5,1.5,az,0,2*%pi),
  surface_hide = true)$

/* adding intersection curves */
scn3: gr3d(
  color       = red,
  spherical(1,a,0,2*%pi,z,0,%pi),
  color       = green,
  cylindrical(1/sqrt(2),z,-1.5,1.5,az,0,2*%pi),
  color       = blue,
  line_width  = 3,
  parametric(cos(t)/sqrt(2),
             sin(t)/sqrt(2), 
             sqrt(1-(cos(t)/sqrt(2))^2-(sin(t)/sqrt(2))^2),
             t,0,2*%pi),
  parametric(cos(t)/sqrt(2),
             sin(t)/sqrt(2), 
             -sqrt(1-(cos(t)/sqrt(2))^2-(sin(t)/sqrt(2))^2),
             t,0,2*%pi),
  surface_hide = true)$

draw(
    columns    = 1,
    terminal   = png,
    dimensions = [300,900],
    scn1,scn2,scn3) $

Now the union and intersection of the sphere and the cylinder:

draw(
  columns    = 1,
  terminal   = eps,
  dimensions = 100*[8,16],
    
  /* union */
  gr3d(enhanced3d   = true,
       implicit(min(x^2+y^2+z^2,2*x^2+2*y^2)=1,
                x,-1.5,1.5,y,-1.5,1.5,z,-1.5,1.5),
       surface_hide = true,
       palette      = gray),

  /* intersection */
  gr3d(enhanced3d   = true,
       implicit(max(x^2+y^2+z^2,2*x^2+2*y^2)=1,
                x,-1.5,1.5,y,-1.5,1.5,z,-1.5,1.5),
       surface_hide = true,
       palette      = gray) )$

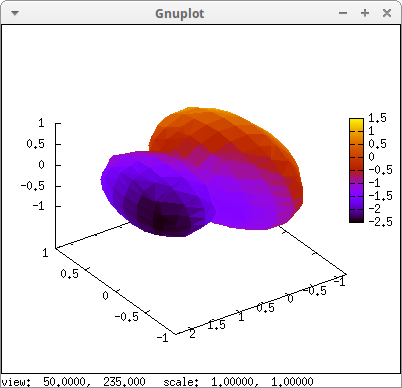
Color numbers for implicit surfaces can be only defined with respect to the \((x, y, z)\) coordinates:

draw3d(
  enhanced3d = [x-y,x,y,z],
  implicit((x^2+y^2+z^2-1)*(x^2+(y-1.5)^2+z^2-0.5)=0.015,
           x,-1,1, y,-1.2,2.3, z,-1,1)) $

© 2011-2016, TecnoStats.