Once you have opened a Maxima session, load package draw:
load("draw") $
To read the documentation on object parametric_surface, write the following sentence:
describe(parametric_surface) $
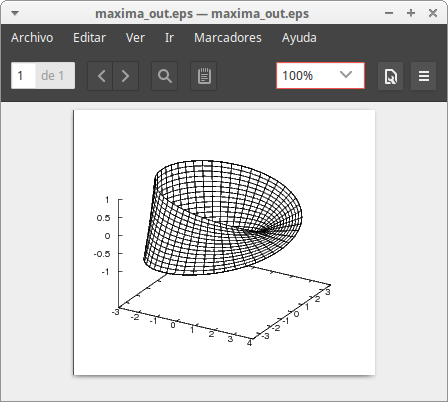
The Möbius band:
draw3d(
xu_grid = 50,
yv_grid = 15,
surface_hide = true,
dimensions = 100*[8,7],
terminal = eps,
parametric_surface(cos(a)*(3+b*cos(a/2)),
sin(a)*(3+b*cos(a/2)),
b*sin(a/2), a,-%pi,%pi,b,-1,1) )$
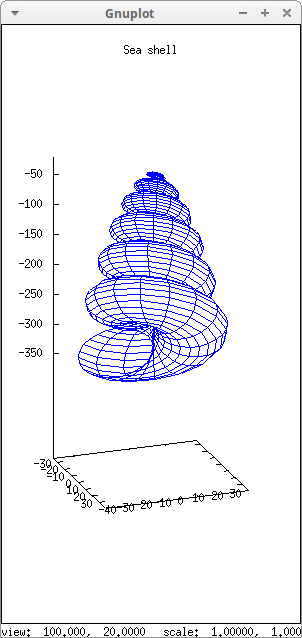
Sea shell:
draw3d(
title = "Sea shell",
dimensions = [300,600],
xu_grid = 100,
yv_grid = 25,
view = [100,20],
surface_hide = true,
parametric_surface(0.5*u*cos(u)*(cos(v)+1),
0.5*u*sin(u)*(cos(v)+1),
u*sin(v) - ((u+3)/8*%pi)^2 - 20,
u, 0, 13*%pi, v, -%pi, %pi) )$
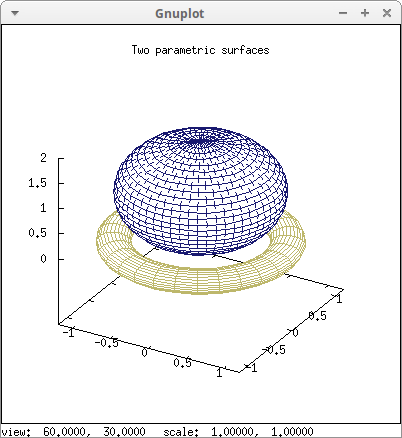
Torus and sphere:
draw3d(
surface_hide = true,
dimensions = [400,400],
title = "Two parametric surfaces",
color = dark_khaki,
parametric_surface((1-0.2*cos(v))*cos(u),
(1-0.2*cos(v))*sin(u),
0.2*sin(v), u,0,2*%pi,v,0,2*%pi),
color = midnight_blue,
parametric_surface(cos(u)*cos(v),
cos(u)*sin(v),
1+sin(u), u,-2*%pi,2*%pi,v,0,2*%pi) )$
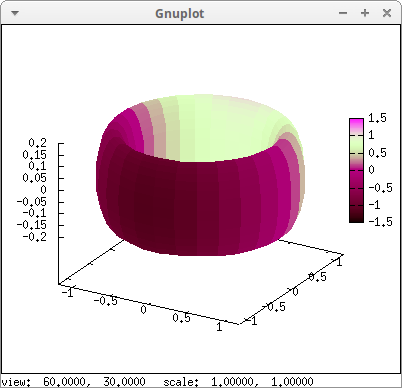
An enhanced torus:
draw3d(
palette = [7,-15,3],
enhanced3d = (1-0.2*cos(v))*sin(u),
parametric_surface(
(1-0.2*cos(v))*cos(u),
(1-0.2*cos(v))*sin(u),
0.2*sin(v),
u, 0, 2*%pi, v, 0, 2*%pi)) $
Interlocking enhanced tori:
draw3d(
enhanced3d = sin(u)+cos(v),
terminal = eps_color,
palette = [8,4,3],
dimensions = 100*[10,10],
parametric_surface(cos(u)+.5*cos(u)*cos(v),
sin(u)+.5*sin(u)*cos(v),
.5*sin(v),
u, -%pi, %pi,
v, -%pi, %pi),
parametric_surface(1+cos(u)+.5*cos(u)*cos(v),
.5*sin(v),
sin(u)+.5*sin(u)*cos(v),
u, -%pi, %pi,
v, -%pi, %pi)) $
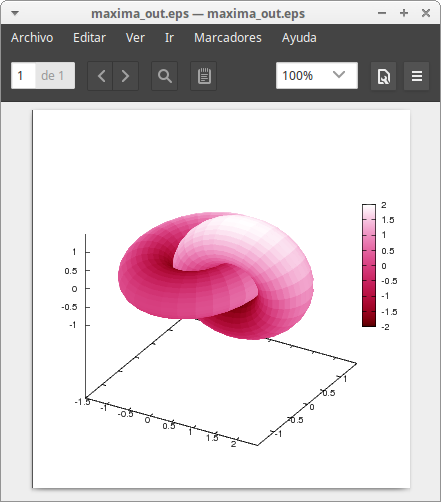
Archimedes would like this one. A cylinder circumscribed on a sphere:
draw3d(
terminal = eps_color,
dimensions = 100*[10,10],
surface_hide = true,
xtics = none,
ytics = none,
ztics = none,
axis_3d = false,
view = [48,22],
parametric_surface(cos(a)*cos(b),
cos(b)*sin(a),
sin(b), a,0,2*%pi,b,-%pi/2,%pi/2),
color = cyan,
parametric_surface(1.01*cos(a),1.01*sin(a),z,a,0,3/2*%pi,z,-1,1),
xu_grid = 25,
yv_grid = 5,
parametric_surface(1.01*r*cos(a),1.01*r*sin(a),1,a,0,3/2*%pi,r,0,1),
parametric_surface(1.01*r*cos(a),1.01*r*sin(a),-1,a,0,3/2*%pi,r,0,1))$
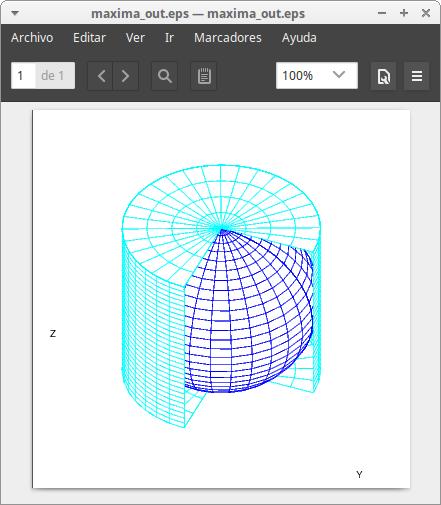
A parametric_surface object is defined in terms of two parameters \((u, v)\); we can define color numbers with respect to them:
load(fractals) $
draw3d(
xu_grid = 200,
yv_grid = 200,
palette = gray,
view = [125,280],
proportional_axes = xyz,
enhanced3d = ['mandelbrot_set(u-%pi,v-%pi/2),u,v],
parametric_surface(
cos(u)*sin(v),
sin(u)*sin(v),
cos(v), u, 0, 2*%pi, v, 0, %pi))$
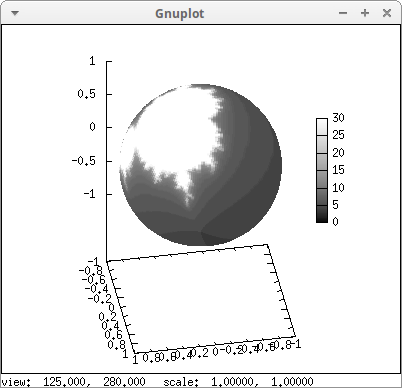
We can define color numbers in terms of coordinates \((x, y, z)\). Suppose a toroidal surface in a 3D scalar field \(\phi = \sin(10 x^2 + 13 y^2 + 7 z^2)\); here is a colored representation of the field values on the surface:
draw3d(
xu_grid = 200,
yv_grid = 200,
enhanced3d = [sin(10*x^2+13*y^2+7*z^2),x,y,z],
proportional_axes = xyz,
parametric_surface(
(1-0.2*cos(v))*cos(u)-1/2,
(1-0.2*cos(v))*sin(u)-1/2,
0.2*sin(v), u, 0, 2*%pi, v, 0, 2*%pi))$
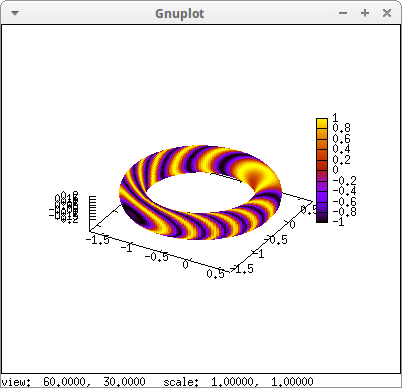
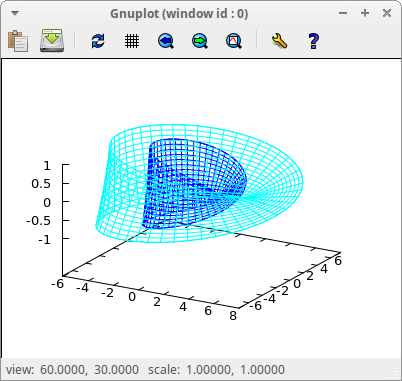
Two Möbius bands:
draw3d(
xu_grid = 50,
yv_grid = 15,
terminal = wxt,
parametric_surface(cos(a)*(3+b*cos(a/2)),
sin(a)*(3+b*cos(a/2)),
b*sin(a/2), a,-%pi,%pi,b,-1,1),
transform = [2*x,2*y,z,x,y,z],
color = cyan,
parametric_surface(cos(a)*(3+b*cos(a/2)),
sin(a)*(3+b*cos(a/2)),
b*sin(a/2), a,-%pi,%pi,b,-1,1) )$
© 2011-2016, TecnoStats.