Along this section, we are going to build interpolation curves, based on cubic splines, passing through a set of arbitrary points spread in space.
First step is to load package interpol,
load("interpol")$
Since we want to show graphical results with the VTK graphics library, let us also load package draw and set the corresponding draw renderer,
load("draw") $
draw_renderer: vtk $
Generate a set of n = 5 random points,
n: 5 $ p: makelist(makelist(random(10),2), n);
\[ \left[ \left[ 9 , 0 \right] , \left[ 9 , 4 \right] , \left[ 7 , 6 \right] , \left[ 9 , 9 \right] , \left[ 3 , 9 \right] \right] \]
Extract the x coordinates and interpolate them by cubic splines,
cs1: cspline(map(first,p), varname=t);
\[ \left(-{{27\,t^3}\over{28}}+{{81\,t^2}\over{28}}-{{27\,t}\over{14}} +9\right)\,{\it charfun_2}\left(t , -\infty , 2\right)+ \\ \left({{69 \,t^3}\over{28}}-{{1035\,t^2}\over{28}}+{{2469\,t}\over{14}}-{{1839 }\over{7}}\right)\,{\it charfun_2}\left(t , 4 , \infty \right)+ \\ \left(-{{121\,t^3}\over{28}}+{{1245\,t^2}\over{28}}-{{2091\,t}\over{ 14}}+{{1201}\over{7}}\right)\,{\it charfun_2}\left(t , 3 , 4\right)+ \\ \left({{79\,t^3}\over{28}}-{{555\,t^2}\over{28}}+{{87\,t}\over{2}}- {{149}\over{7}}\right)\,{\it charfun_2}\left(t , 2 , 3\right) \]
Function charfun_2 returns 1 if the first argument belongs to the interval defined by the other two arguments.
Now, the same procedure with the y coordinates
cs2: cspline(map(second,p), varname=t);
\[ \left(-{{37\,t^3}\over{56}}+{{111\,t^2}\over{56}}+{{75\,t}\over{28 }}-4\right)\,{\it charfun_2}\left(t , -\infty , 2\right)+ \\ \left({{ 51\,t^3}\over{56}}-{{765\,t^2}\over{56}}+{{1887\,t}\over{28}}-{{702 }\over{7}}\right)\,{\it charfun_2}\left(t , 4 , \infty \right)+ \\ \left(-{{87\,t^3}\over{56}}+{{891\,t^2}\over{56}}-{{1425\,t}\over{28 }}+{{402}\over{7}}\right)\,{\it charfun_2}\left(t , 3 , 4\right)+ \\ \left({{73\,t^3}\over{56}}-{{549\,t^2}\over{56}}+{{105\,t}\over{4}}- {{138}\over{7}}\right)\,{\it charfun_2}\left(t , 2 , 3\right) \]
Let's plot our results,
draw2d( point_type = circle, points(p), nticks = 70, color = red, parametric(cs1,cs2, t, 1, n)) $
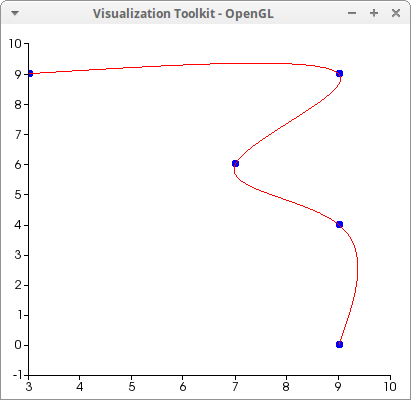
If we want to interpolate at \(t=2.5\),
ev([cs1,cs2], t=2.5);
\[ \left[ 7.665178571428569 , 5.006696428571427 \right] \]
Just as in the 2D example, let Maxima generate n = 5 random points in the three dimensional world,
n: 5 $ p: makelist(makelist(random(10),3), n);
\[ \left[ \left[ 2 , 2 , 4 \right] , \left[ 5 , 4 , 1 \right] , \left[ 9 , 5 , 8 \right] , \left[ 3 , 5 , 5 \right] , \left[ 0 , 6 , 9 \right] \right] \]
Extract the x, y, and z coordinates,
cs1: cspline(map(first,p),varname=t) $ cs2: cspline(map(second,p),varname=t) $ cs3: cspline(map(third,p),varname=t) $
Plot the parametric curve passing through the random points,
draw3d( point_type = sphere, point_size = 0.5, points(p), line_type = tube, color = yellow, line_width = 0.1, parametric(cs1,cs2,cs3, t, 1, 5)) $
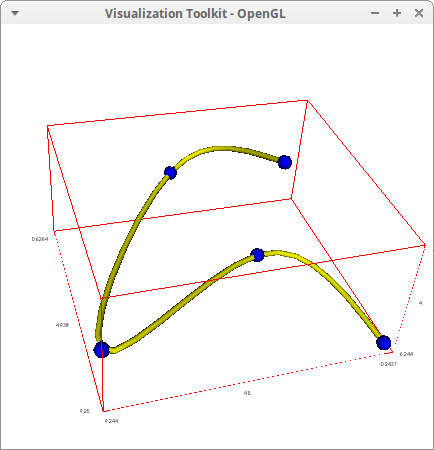
Interpolation at \(t=2.5\),
ev([cs1,cs2,cs3], t=2.5);
\[ \left[ 7.790178571428569 , 4.674107142857142 , 4.707589285714292 \right] \]
© 2016, TecnoStats.