The following table contains different velocity measures of a flying object, the first column corresponds to the moments of observations in seconds, and the second column to velocities in meters per second.
| Time (s) | Velocity (m/s) |
|---|---|
| 0 | 0 |
| 10 | 25 |
| 15 | 36 |
| 20 | 68 |
| 25 | 93 |
| 30 | 97 |
| 35 | 99 |
Let's introduce these data into Maxima and see how they look like,
table: [[0,0], [10,25], [15,36], [20,68], [25,93], [30,97], [35,99]]$ load(draw)$ draw2d( points_joined = true, grid = true, points(table)) $
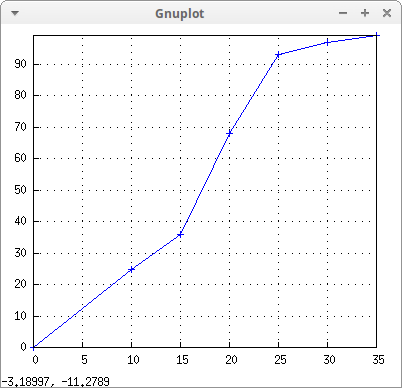
Observed data are joined by segments or linear interpolators, we can take advantage of them to estimate velocities in any point between 0 and 35 seconds.
load("interpol") $
lin: linearinterpol(table, varname=t);
\[ {{5\,t\,{\it charfun_2}\left(t , -\infty , 10\right)}\over{2}}+ \left({{2\,t}\over{5}}+85\right)\,{\it charfun_2}\left(t , 30 , \infty \right)+ \\ \left({{4\,t}\over{5}}+73\right)\,{\it charfun_2} \left(t , 25 , 30\right)+\left(5\,t-32\right)\,{\it charfun_2}\left( t , 20 , 25\right)+ \\ \left({{32\,t}\over{5}}-60\right)\, {\it charfun_2}\left(t , 15 , 20\right)+\left({{11\,t}\over{5}}+3 \right)\,{\it charfun_2}\left(t , 10 , 15\right) \]
In the result above, function charfun_2 is defined in package interpol and returns 1 if the first argument belongs to the interval defined by the other two arguments.
If we want an estimation of the velocity of the flying object at \(t=7 s\) and \(t=24 s\), we can define a function,
v1(t) := ''lin $ [v1(7), v1(24)] ;
\[ \left[ {{35}\over{2}} , 88 \right] \]
In case we prefer a smooth function for interpolation, an alternative is the Lagrangian polynomial,
lag: lagrange(table, varname=t);
\[{{33\,\left(t-30\right)\,\left(t-25\right)\,\left(t-20\right)\, \left(t-15\right)\,\left(t-10\right)\,t}\over{4375000}}- \\ {{97\,\left( t-35\right)\,\left(t-25\right)\,\left(t-20\right)\,\left(t-15\right) \,\left(t-10\right)\,t}\over{2250000}}+\\ {{31\,\left(t-35\right)\, \left(t-30\right)\,\left(t-20\right)\,\left(t-15\right)\,\left(t-10 \right)\,t}\over{312500}}-\\ {{17\,\left(t-35\right)\,\left(t-30\right) \,\left(t-25\right)\,\left(t-15\right)\,\left(t-10\right)\,t}\over{ 187500}}+\\ {{\left(t-35\right)\,\left(t-30\right)\,\left(t-25\right)\, \left(t-20\right)\,\left(t-10\right)\,t}\over{31250}}-\\ {{\left(t-35 \right)\,\left(t-30\right)\,\left(t-25\right)\,\left(t-20\right)\, \left(t-15\right)\,t}\over{150000}}\]
This is a sixth degree polynomial,
lag: expand(lag);
\[ -{{67\,t^6}\over{39375000}}+{{92\,t^5}\over{328125}}-{{1051\,t^4 }\over{63000}}+{{2351\,t^3}\over{5250}}-{{168359\,t^2}\over{31500}}+ {{13238\,t}\over{525}} \]
We interpolate again for \(t=7 s\) and \(t=24 s\),
v2(t) := ''lag $ [v2(7), v2(24)] ;
\[ \left[ {{2552418}\over{78125}} , {{7003392}\over{78125}} \right] \]
Let's now add the Lagrange polynomial to our plot of observed data,
draw2d( points_joined = true, grid = true, points(table), color = red, explicit (v2(t),t,0,35)) $
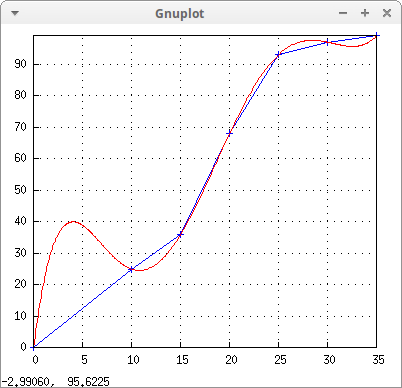
As is easily seen, the Lagrange polynomial can be a bad interpolator near the boundaries of the experimental data.
In case we want an estimation of the instantaneous acceleration in \(t=17\), since \(a(t)=\frac{d v(t)}{d t}\), we can differentiate the interpolator,
/* in m/s^2 */ float(subst(t=17, diff(v2(t),t)));
\[ 6.492423771428571 \]
The mean velocity during time interval \([10,25]\), defined as \(\frac{1}{25-10} \int_{10}^{25} v(t) dt\), is
/* in m/s */ float(integrate(v2(t),t, 10, 25) / (25-10));
\[ 53.77636054421769 \]
The distance covered during this time interval is given by \(\int_{10}^{25} v(t) dt\), which is equal to
/* in m */ float(integrate(v2(t),t, 10, 25));
\[ 806.6454081632653 \]
© 2016, TecnoStats.