Atractores

Investigamos el comportamiento asintótico de ciertas sucesiones recursivas.

Trabajaremos con la siguiente sucesión definida de forma recursiva: $$\left\{ \begin{array}{ll} a_0 \\ a_n = c \cdot a_{n-1} (1 - a_{n-1}) \end{array} \right.$$ siendo $c$ una constante y $a_0$ su valor inicial, ambos conocidos. La ecuación se utiliza en algunos modelos sobre dinámica poblacional.

En primer lugar, calculamos los $n=50$ primeros términos de la sucesión que tiene como término inicial $a_0=\frac{1}{2}$ y constante $c=\frac{9}{10}$. Usaremos las variables globales numer y fpprintprec para forzar que los cálculos sean todos numéricos y que los números decimales se muestren con pocos dígitos; así ganamos en rapidez y claridad.

numer: true $
fpprintprec: 4 $

/* fijamos parametros */
a[0]: 1/2 $
c: 9/10 $
n: 50 $
a[k]:= c * a[k-1] * (1-a[k-1]) $
s: makelist(a[i],i,0,n) $

/* generamos el grafico */
draw2d(
    points_joined = true,
    grid          = true,
    points(s) ) $

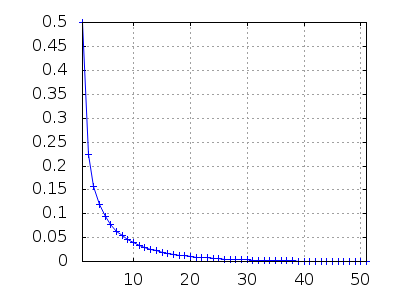
La representación gráfica que obtenemos nos induce a pensar que los términos de la sucesión se acercan cada vez más a cero. Se trata de un caso de sucesión convergente.

Estudiamos el caso para $a_0=1.1$, $c=-2.1$ y $n=15$ términos,

numer: true $
fpprintprec: 4 $

/* fijamos parametros */
a[0]: 1.1 $
c: -2.1 $
n: 15 $
a[k]:= c * a[k-1] * (1-a[k-1]) $
s: makelist(a[i],i,0,n) $

/* generamos el grafico */
draw2d(
    points_joined = true,
    grid          = true,
    points(s) ) $

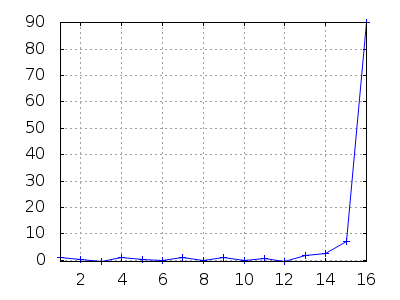
Los valres se disparan a partir de la posición 15; se dice que la sucesión es divergente.

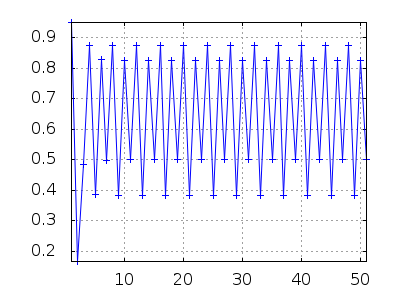
En el caso de $a_0=\frac{19}{20}$, $c=\frac{7}{2}$ y $n=50$ términos, los valores que toma la sucesión se concentran en cuatro puntos, repitiendo siempre el mismo patrón. Se dice que tiene un atractor cíclico de orden 4. Veámoslo,

numer: true $
fpprintprec: 4 $

/* fijamos parametros */
a[0]: 19/20 $
c: 7/2 $
n: 50 $
a[k]:= c * a[k-1] * (1-a[k-1]) $
s: makelist(a[i],i,0,n) $

/* generamos el grafico */
draw2d(
    points_joined = true,
    grid          = true,
    points(s) ) $

Examinamos ahora el comportamiento para $a_0=\frac{1}{5}$, $c=4$ y $n=100$.

numer: true $
fpprintprec: 4 $

/* fijamos parametros */
a[0]: 1/5 $
c: 4 $
n: 100 $
a[k]:= c * a[k-1] * (1-a[k-1]) $
s: makelist(a[i],i,0,n) $

/* generamos el grafico */
draw2d(
    points_joined = true,
    grid          = true,
    points(s) ) $

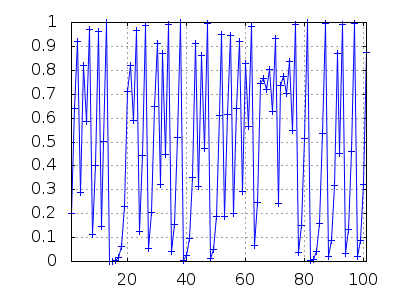
Esta sucesión ni converge a un punto, ni es divergente, ni tiene tampoco un atractor cíclico; su comportamiento es, simplemente, impredecible; es un caso de atractor caótico.

© 2011-2016, TecnoStats.