Direction fields

• Single differential equation
• System of differential equations

We want to plot direction fields of first order differential equations defined by means of \[ \frac{dy}{dx}= F(x,y), \] or of \[ \left\{ \begin{array}{ccl} \frac{dx}{dt} & = & G(x,y) \\ \frac{dy}{dt} & = & F(x,y) \end{array} \right. \]

In both cases, we need to load package drawdf,

load("drawdf")$

Single differential equation

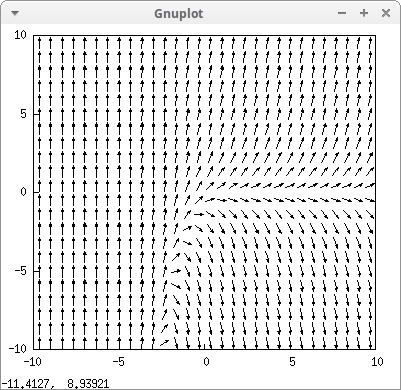
First example is the differential equation \[ \frac{dy}{dx}= \exp(-x)+y, \] where the independent and dependent variables are x and y, respectively.

drawdf(exp(-x)+y)$

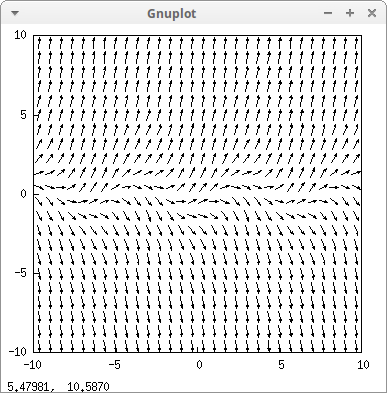
In case we work with other variables, it's necessary to explicitly declare them. For example, the direction field defined by \[ \frac{dy}{dt}= \cos(-t)+y, \] is plotted as follows,

drawdf(cos(-t)+y, [t,y])$

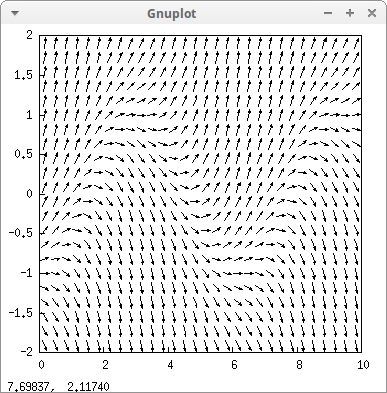
The default plotting range is \([-10,10] \times [-10,10]\), but it's possible to change it,

drawdf(cos(-t)+y, [t,0,10], [y,-2,2])$

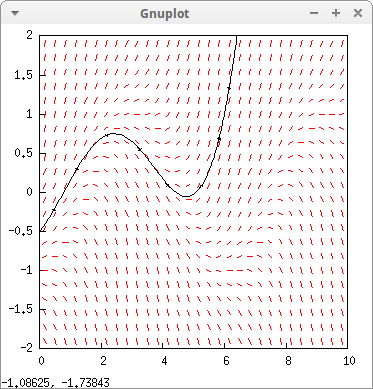
We can add to the direction field the trajectory passing through a particular point, (6,1),

drawdf(
  cos(-t)+y, [t,0,10], [y,-2,2],
  soln_arrows = true,
  soln_at(6,1))$

We can make use of ordinary draw package options to costumize the plot,

drawdf(
  cos(-t)+y, [t,0,10], [y,-2,2],
  line_width       = 3,
  color            = blue,
  solns_at([6,1], [4,-1]),
  color            = yellow,
  background_color = light_gray,
  soln_at(9,-1) ) $

To change the number of columns and rows in the grid, use option field_grid. Also, setting field_degree=2 forces arrows to be substituted by quadratic splines,

drawdf(
  cos(-t)+y, [t,0,10], [y,-2,2],

  field_degree     = 2,
  field_grid       = [15,10],

  line_width       = 3,
  color            = blue,
  solns_at([6,1], [4,-1]),
  color            = yellow,
  background_color = light_gray,
  soln_at(9,-1),
 
  /* Plot interesting points */
  points_joined = false,
  color = black,
  point_type = filled_circle,
  point_size = 1.5,
  points([[6,1], [4,-1], [9,-1]]),
  
  /* Labels and title */
  xlabel = "t",
  ylabel = "y",
  title  = "Direction field of single diff. eq.")$

System of differential equations

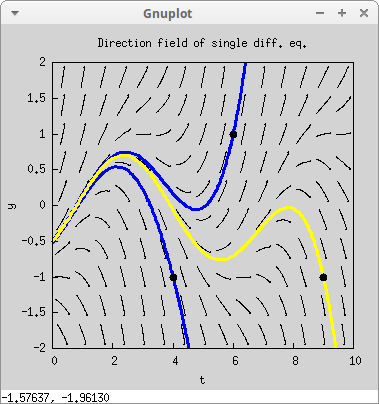
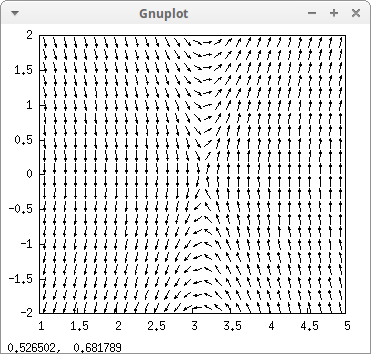
Let's now try the system \[ \left\{ \begin{array}{ccl} \frac{dx}{dt} & = & y \\ \frac{dy}{dt} & = & -9 \sin(x)-\frac{y}{5} \end{array} \right. \]

drawdf([y,-9*sin(x)-y/5], [x,1,5], [y,-2,2])$

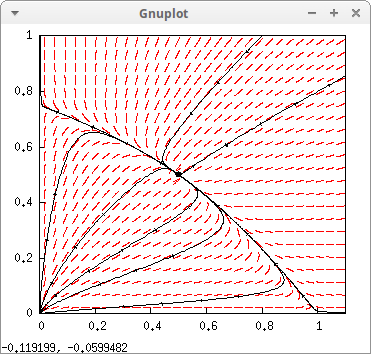
Now, the direction field for \[ \left\{ \begin{array}{ccl} \frac{dx}{dt} & = & x (1-x-y) \\ \frac{dy}{dt} & = & y (\frac{3}{4}-y-\frac{x}{2}) \end{array} \right. \]

drawdf(
  [x*(1-x-y), y*(3/4-y-x/2)], [x,0,1.1], [y,0,1],
  field_degree = 2,
  duration     = 40,
  soln_arrows  = true,
  point_at(1/2,1/2),
  solns_at([0.1,0.2], [0.2,0.1], [1,0.8], [0.8,1],
           [0.1,0.1], [0.6,0.05], [0.05,0.4],
           [1,0.01], [0.01,0.75]))$

Finally, for more information on package drawdf, write

? drawdf

© 2011-2016, TecnoStats.