
Un conjunto de componentes tecnológicos se dice que están conectados en serie cuando basta que falle uno de ellos cualquiera para que falle también el sistema, se representa con el siguiente diagrama de bloques,

Cada componente Xi se supone que tiene un tiempo de supervivencia con distribución Weibull de parámetros ai y bi, todos independientes entre sí, por lo que Si(t)=Pr es la función de fiabilidad de la i-ésima componente y h_i(t)=\frac{a_i}{b_i} \left( \frac{t}{b_i} \right)^{a_i-1} es su tasa de fallo.
La función de fiabilidad del sistema completo viene dada por S(t) = \prod_{i=1}^n S_i(t) = \exp\left[-\sum_{i=1}^n \left(\frac{t}{b_i} \right)^{a_i} \right], donde se ha tenido en cuenta que los fallos de las componentes ocurren de forma independiente.
La tasa de fallo del sistema viene dada por h(t)=-\frac{d \log(S(t))}{dt}=\sum_{i=1}^n \frac{a_i}{b_i} \left(\frac{t}{b_i} \right)^{a_i} = \sum_{i=1}^n h_i(t), por lo que se reduce a la suma de las tasas de fallo de cada una de las componentes que forman el sistema en serie.
Veamos un cálculo con Maxima para tres elementos Weibull en serie con parámetros ai y bi. Empezamos por la función de supervivencia,
S(t,a,b) :=
block([n: length(a)],
prod(exp(-(t/b[k])^a[k]),k,1,n) ) $
S(t, [a1, a2, a3], [b1, b2, b3]);
e^{-\left({{t}\over{{\it b_3}}}\right)^{{\it a_3}}-\left({{t}\over{ {\it b_2}}}\right)^{{\it a_2}}-\left({{t}\over{{\it b_1}}}\right)^{ {\it a_1}}}
Continuamos con la tasa de riesgo,
h(t,a,b) :=
block([n: length(a)],
sum(a[k]/b[k]*(t/b[k])^(a[k]-1),k,1,n) ) $
h(t, [a1, a2, a3], [b1, b2, b3]);
{{{\it a_3}\,\left({{t}\over{{\it b_3}}}\right)^{{\it a_3}-1} }\over{{\it b_3}}}+{{{\it a_2}\,\left({{t}\over{{\it b_2}}}\right)^{ {\it a_2}-1}}\over{{\it b_2}}}+{{{\it a_1}\,\left({{t}\over{ {\it b_1}}}\right)^{{\it a_1}-1}}\over{{\it b_1}}}
Si los parámetros del primer componente son a1=0.92 y b1=0.35, los del segundo a2=0.10 y b2=0.26 y los del tercero a3=2.81 y b3=1.62, podemos ver los gráficos correspondientes de la función de supervivencia y de la tasa de riesgo,
a: [0.92, 0.10, 2.81] $
b: [0.35, 0.26, 1.62] $
load(draw) $
draw2d(
grid = true,
explicit(S(t,a, b), t, 0.01, 3)) $
draw2d(
grid = true,
yrange = [0,9],
explicit(h(t,a, b), t, 0.01, 3)) $
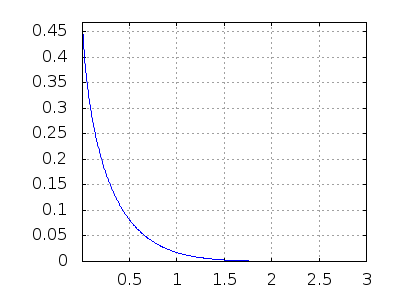
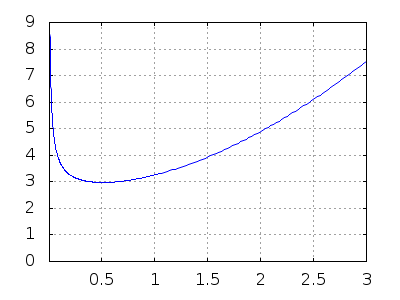
Como se ve, la tasa de riesgo del sistema formado por estos tres componentes adquiere un patrón en forma de bañera.
Por último, el tiempo medio de fallo del sistema, \mbox{MTTF} = E[T] = \int_0^\infty t f(t) dt, siendo f(t)=-\frac{d}{dt}S(t), se obtiene por métodos de cuadratura numérica,
u: t*diff(-S(t, a, b), t) $ quad_qagi(u,t,0,inf)[1] ;
0.12898798715318
Un conjunto de componentes tecnológicos se dice que están conectados en paralelo cuando es necesario que fallen todos ellos para que falle también el sistema, se representa con el siguiente diagrama de bloques,
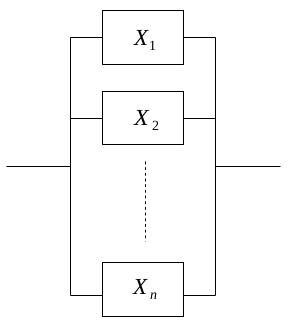
Cada una de las n componentes Xi se supone que tiene un tiempo de supervivencia con distribución Weibull de parámetros ai y bi, todos independientes entre sí.
La función de fiabilidad del sistema completo viene dada por S(t)=1-\prod_{i=1}^n (1-S_i(t))=1-\prod_{i=1}^n \left( 1-\exp\left( -\left( \frac{t}{b_i} \right)^{a_i} \right) \right), donde se ha tenido en cuenta que los fallos de las componentes ocurren de forma independiente.
La tasa de fallo del sistema viene dada por h(t) = \frac{1}{S(t)} \sum_{i=1}^n \prod_{i=1}^n Q_{ij}(t), donde Q_{ij}(t)= \left\{ \begin{array}{ll} F_j(t) & \mbox{ si \(j \neq i\)} \\ f_j(t) & \mbox{ si \(j = i\)} \end{array} \right. siendo F_j(t) y f_j(t) las funciones de distribución y de densidad, respectivamente, de la j-ésima componente, con modelo Weibull de parámetros aj y bj.
Los sistemas con arquitectura paralelo se suelen utilizar para aumentar la fiabilidad del conjunto.
Un conjunto de componentes tecnológicos se dice que están conectados en serie-paralelo cuando es dispone de varios subsistemas en serie conectados en paralelo, se representa con el siguiente diagrama de bloques,
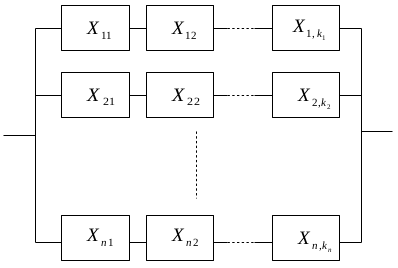
Cada una de las \sum_{i=1}^n k_{i} componentes Xij se supone que tiene un tiempo de supervivencia con distribución exponencial de parámetro λij, produciéndose los fallos de forma independiente entre los elementos. Reservamos el parámetro i para referenciar los ramales paralelos y j para las componentes de las series.
Teniendo en cuenta que tratamos con un modelo exponencial, S_{ij}(t)= \Pr(T_{ij} \gt t) = e^{-\lambda_{ij} t}, \forall i,j, es la función de fiabilidad de cualquiera de sus componentes y h_{ij}(t)= \lambda_{ij} es su tasa de fallo constante.
La función de fiabilidad del sistema completo viene dada por \begin{array}{lcl} S(t) & = & 1-\prod_{i=1}^n \left(1-\prod_{j=1}^{k_i} S_{ij}(t)\right) \\ & = & 1-\prod_{i=1}^n \left(1- \exp\left( -\sum_{j=1}^{k_i} \lambda_{ij}t \right) \right), \end{array} donde se ha tenido en cuenta que los fallos de las componentes ocurren de forma independiente.
La tasa de fallo del sistema viene dada por h(t)= \frac{f(t)}{S(t)}, donde f(t)=-\frac{d}{dt}S(t) es la función de densidad del tiempo de fallo del sistema, cuya expresión es laboriosa de desarrollar.
Un conjunto de componentes tecnológicos se dice que están conectados en paralelo-serie cuando es dispone de varios subsistemas en paralelo conectados en serie, se representa con el siguiente diagrama de bloques,
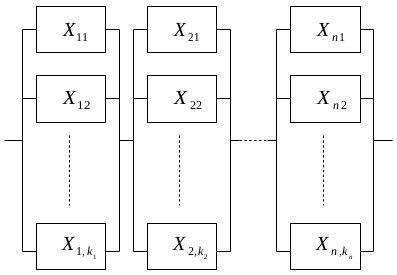
Cada una de las \sum_{i=1}^n k_{i} componentes Xij se supone que tiene un tiempo de supervivencia con distribución exponencial de parámetro λij, produciéndose los fallos de forma independiente entre los elementos. Reservamos el parámetro i para referenciar los sistemas conectados en serie y j para las componentes de cada subsistema paralelo.
Teniendo en cuenta que tratamos con un modelo exponencial, S_{ij}(t)= \Pr(T_{ij} \gt t) = e^{-\lambda_{ij} t}, \forall i,j, es la función de fiabilidad de cualquiera de sus componentes y h_{ij}(t)= \lambda_{ij} es su tasa de fallo constante.
La función de fiabilidad del sistema completo viene dada por \begin{array}{lcl} S(t) & = & \prod_{i=1}^n \left(1-\prod_{j=1}^{k_i} (1-S_{ij}(t))\right) \\ & = & \prod_{i=1}^n \left(1-\prod_{j=1}^{k_i} (1-\exp\left(-\lambda_{ij}t) \right) \right), \end{array} donde se ha tenido en cuenta que los fallos de las componentes ocurren de forma independiente.
La tasa de fallo del sistema viene dada por h(t)= \frac{f(t)}{S(t)}, donde f(t)=-\frac{d}{dt}S(t) es la función de densidad del tiempo de fallo del sistema, cuya expresión es laboriosa de desarrollar.
© 2011-2016, TecnoStats.