Método del camino crítico

El método CPM (Critical Path Method), o método del camino crítico, es un algoritmo para la planificación de proyectos en los que están involucradas un serie de fases, cada una con una duración determinada, y con un cierto orden de ejecución que es necesario respetar. La metodología se inscribe dentro de la categoría de técnicas de optimización de grafos.

El resultado que ofrece el algoritmo es el camino crítico, la sucesión de fases que bajo ningún concepto se pueden demorar en el tiempo, ya que ello implicaría un retraso en la ejecución del proyecto completo.

También el algoritmo nos permite detectar aquellas tareas con holguras en el tiempo, esto es, fases del proyecto que admiten cierto retraso sin que ello afecte al tiempo de ejecución del proyecto en su conjunto.

Puesto que de grafos hablamos, debemos cargar primero en memoria la librería correspondiente,

load("graphs") $

El planteamiento del problema requiere indicar las fases, del proyecto, así como sus respectivas duraciones en el tiempo y las tareas que requieren de su terminación para ellas mismas poder iniciar su ejecución. La tabla siguiente acoge un sencillo ejemplo sobre la elaboración de un plan para la construcción de una pista deportiva:

Actividad	Descripción	Días	Precede a
A	Desbrozar el terreno	5	B, D, E
B	Explanar	10	C
C	Asfaltar	25	G
D	Instalar augua e luz	30	G
E	Pintado de pistas	15	F
F	Peche das pistas	20	H
G	Colocación mobiliario	5	H
H	Iluminación e señais	10	--

Los datos anteriores definen un grafo dirigido en el que cada fase se asocia a un arco y a una etiqueta que es el tiempo necesario para completar su ejecución,

[A,B,C,D,E,F,G,H]: makelist(k,k,1,8) $

g: create_graph(
    [[A,5],[B,10],[C,25],[D,30],[E,15],[F,20],[G,5],[H,10]],
    [[A,B], [A,D], [A,E], [B,C], [C,G], [D,G], [E,F], [F,H], [G,H]],
    directed=true);

DIGRAPH(8 vertices, 9 arcs)

Representamos gráficamente el problema que se nos ha presentado,

draw_graph(g, 
    show_id       = true, 
    show_vertices = vertices (g),
    file_name     = "grafo1",
    terminal      = png) $

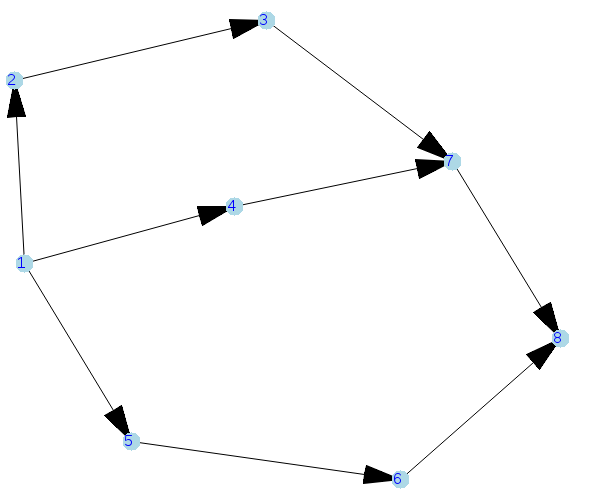
Para hacer el cálculo de la ruta crítica necesitamos programar el algoritmo,

cpm(g) :=
    block([ta, p, c, nv, start, end],
        if not is_digraph(g) then error("Grafo no dirigido"),
        nv: graph_order (g),
        p: makelist(in_neighbors (k, g), k, 1, nv),
        c: makelist(out_neighbors (k, g), k, 1, nv),
        block([nc,np],
            nc: sublist_indices (c, lambda ([z], z='[])),
            np: sublist_indices (p, lambda ([z], z='[])),
            if length(nc) # 1 
              then error("Debe haber exactamente un nodo sin hijos"),
            if length(np) # 1
              then error("Debe haber exactamente un nodo sin padres"),
            start: first(np),
            end: first(nc)  ),
        ta: makelist([-1,-1,0], k, nv),
        local(early, late, critical_path),
        early(n):=
            block([],
                for j in p[n] do if ta[j][1] < 0 then early(j),
                ta[n][1] : lmax(makelist(ta[k][1] + get_vertex_label(n, g),
                                         k, p[n])) ),
        late(n):=
            block([],
                for j in c[n] do if ta[j][2] < 0 then late(j),
                ta[n][2] : lmin(makelist(ta[k][2] - get_vertex_label(k, g),
                                         k, c[n])) ),
        
        ta[start][1]: get_vertex_label(start,g),
        early(end),
        ta[end][2]: ta[end][1],
        late(start),
        for k:1 thru nv do
            /* ta[k][3] es la holgura del nodo k */
            ta[k][3]: ta[k][2] - ta[k][1],
    
        critical_path(n):=
            if n = end
              then []
              else block([aux],
                     aux: first(sublist(c[n], lambda([z], last(ta[z])=0))),
                     cons([n,aux], critical_path(aux))),
        critical_path(start))$

Ahora que disponemos de una función para el cálculo del camino crítico, hacemos uso de ella,

ruta: cpm(g);

\[ \left[ \left[ 1 , 2 \right] , \left[ 2 , 3 \right] , \left[ 3 , 7 \right] , \left[ 7 , 8 \right] \right] \]

El programa crea la secuencia de arcos que se deben seguir para alcanzar el punto final del proyecto a partir del estado inicial de manera que se puedan cumplir todas las fases en un tiempo mínimo.

Incorporamos la información anterior a un gráfico y resaltamos la ruta crítica,

draw_graph(g, 
    show_id       = true,
    text_color    = red,
    show_edges    = ruta,
    show_vertices = vertices (g),
    file_name     = "grafo2",
    terminal      = png) $

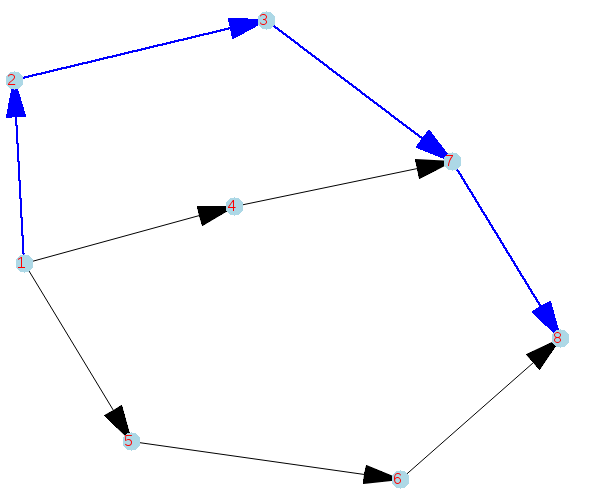
Las fases críticas del proyecto son

fases: cons(part(ruta,1,1),
            makelist(second(ruta[k]),k,length(ruta)));

\[ \left[ 1 , 2 , 3 , 7 , 8 \right] \]

Y el tiempo mínimo de ejecución del proyecto es

apply("+", makelist(get_vertex_label (k, g),k,fases));

\[ 55 \]