En general, la mayor parte de las ecuaciones se resuelven en Maxima con la función solve.
Empezamos por calcular una ecuación de primer grado, \[\frac{4 x-6}{10}+ 2 x= 21 - \frac{3 (x+1)}{12}\]
solve( (4*x-6)/10 + 2*x = 21 - (3*(x+1))/12 );
\[\left[ x={{427}\over{53}} \right]\]
Una ecuación de segundo grado, \[ x^2 - 512 x +6000=0 \]
solve( x^2 - 512*x +6000=0);
\[\left[ x=12 , x=500 \right]\]
Una ecuación de tercer grado, \[ x^3 + 3 x^2 + x-6=0 \]
s: solve( x^3 + 3*x^2 + x-6=0);
\[\left[ x={{2\,\left({{\sqrt{3}\,i}\over{2}}-{{1}\over{2}}\right) }\over{3\,\left({{\sqrt{643}}\over{2\,3^{{{3}\over{2}}}}}+{{5}\over{ 2}}\right)^{{{1}\over{3}}}}}+\left({{\sqrt{643}}\over{2\,3^{{{3 }\over{2}}}}}+{{5}\over{2}}\right)^{{{1}\over{3}}}\,\left(-{{\sqrt{3 }\,i}\over{2}}-{{1}\over{2}}\right)-1 , \\ x=\left({{\sqrt{643}}\over{2 \,3^{{{3}\over{2}}}}}+{{5}\over{2}}\right)^{{{1}\over{3}}}\,\left({{ \sqrt{3}\,i}\over{2}}-{{1}\over{2}}\right)+{{2\,\left(-{{\sqrt{3}\,i }\over{2}}-{{1}\over{2}}\right)}\over{3\,\left({{\sqrt{643}}\over{2 \,3^{{{3}\over{2}}}}}+{{5}\over{2}}\right)^{{{1}\over{3}}}}}-1 , \\ x= \left({{\sqrt{643}}\over{2\,3^{{{3}\over{2}}}}}+{{5}\over{2}}\right) ^{{{1}\over{3}}}+{{2}\over{3\,\left({{\sqrt{643}}\over{2\,3^{{{3 }\over{2}}}}}+{{5}\over{2}}\right)^{{{1}\over{3}}}}}-1 \right]\]
Si la interpretación se hace dificultosa, siempre se puede pasar a formato decimal,
float(expand(s));
\[\left[ x=-1.135939889088928\,i-2.047275740771164 , \\ x= 1.135939889088928\,i-2.047275740771164 , \\ x=1.094551481542327 \right]\]
Resolvemos un sistema lineal de dos incógnitas \[ \left\{ \begin{array}{lcl} \frac{u}{3} + \frac{v-1}{2} & = & -3 \\ 3 (u+v) + v & = & 10 - v \end{array} \right. \]
solve([u/3 + (v-1)/2 = -3, 3*(u+v) + v = 10 - v],
[u, v] );
\[\left[ \left[ u=-105 , v=65 \right] \right]\]
Un sistema no lineal con parámetro, \[ \left\{ \begin{array}{lcl} x y & = & 7 \\ x^2 +y^2 & = & a \end{array} \right. \]
solve([x*y = 7, x^2 +y^2 = a], [x,y]);
\[\left[ \left[ x=-{{\sqrt{\sqrt{a^2-196}+a}}\over{\sqrt{2}}} , y=-{{ 7\,\sqrt{2}}\over{\sqrt{\sqrt{a-14}\,\sqrt{a+14}+a}}} \right] , \\ \left[ x={{\sqrt{\sqrt{a^2-196}+a}}\over{\sqrt{2}}} , y={{7\,\sqrt{2 }}\over{\sqrt{\sqrt{a-14}\,\sqrt{a+14}+a}}} \right] , \\ \left[ x=-{{ \sqrt{a-\sqrt{a^2-196}}}\over{\sqrt{2}}} , y=-{{7\,\sqrt{2}}\over{ \sqrt{a-\sqrt{a-14}\,\sqrt{a+14}}}} \right] , \\ \left[ x={{\sqrt{a- \sqrt{a^2-196}}}\over{\sqrt{2}}} , y={{7\,\sqrt{2}}\over{\sqrt{a- \sqrt{a-14}\,\sqrt{a+14}}}} \right] \right]\]
Estudiamos algebraica y gráficamente los puntos de corte entre la parábola \(y=x^2 + 3 x + 2\) y la recta \(y = 2 x + 3\),
sol: solve([y=x^2 + 3*x + 2, y=2*x + 3], [x,y]);
\[ \left[ \left[ x=-{{\sqrt{5}+1}\over{2}} , y=2-\sqrt{5} \right] , \left[ x={{\sqrt{5}-1}\over{2}} , y=\sqrt{5}+2 \right] \right] \]
Transformamos a decimales,
float(sol);
\[ \left[ \left[ x=-1.618033988749895 , y=-0.2360679774997898 \right] \\ , \left[ x=0.6180339887498949 , y=4.23606797749979 \right] \right] \]
Comprobamos gráficamente,
draw2d( grid = true, background_color = "#f0e68c", explicit(x^2 + 3*x + 2, x, -3, 2), color = red, explicit(2*x + 3, x, -3, 2) ) $
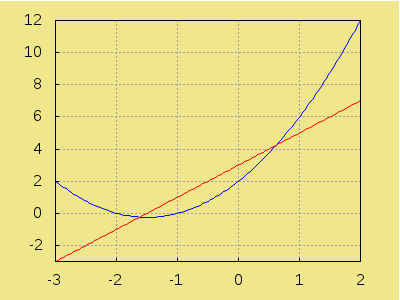
Para las inecuaciones, necesitamos cargar la librería fourier_elim. Empezamos con una inecuación de una sola incógnita, \[ x^4+5 x^3+5 x^2-5 x-6 \geq 0 \]
load("fourier_elim") $
fourier_elim([x^4+5*x^3+5*x^2-5*x-6 > 0], [x]);
\[\left[ 1\lt x \right] \lor \left[ -2\lt x , x\lt -1 \right] \lor \left[ x\lt -3 \right]\]
Resolvemos un sistema de inecuaciones con dos incógnitas, \[ \left\{ \begin{array}{lcl} 3 x - 5 y & \lt & 2 \\ x+y & \gt & \frac{1+x}{3} \\ y & \gt & 2 \end{array} \right. \]
des1 : 3*x - 5*y < 2 $ des2 : x+y> (1+x)/3 $ des3 : y < 2 $ fourier_elim([des1, des2, des3],[x,y]);
\[\left[ {{1}\over{2}}-{{3\,y}\over{2}}\lt x , x\lt {{5\,y}\over{3}}+ {{2}\over{3}} , -{{1}\over{19}}\lt y , y\lt 2 \right]\]
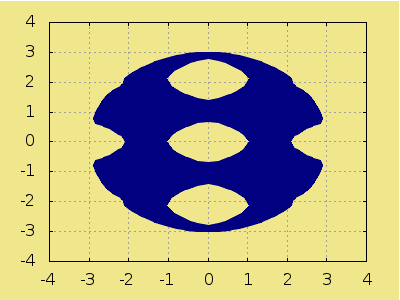
Si el sistema es muy complicado siempre podemos echar mano de la resolución gráfica. Por ejemplo, \[ \left\{ \begin{array}{lcl} \cos(2 x)+\cos(3 y) & \lt & \frac{1}{2} \\ x^2+y^2 & \leq & 9 \end{array} \right. \]
Cargamos el paquete draw y utilizamos el objeto gráfico region,
in1: cos(2*x)+cos(3*y)<1/2 $
in2: x^2+y^2 <=9 $
load("draw") $
draw2d(
x_voxel = 30,
y_voxel = 30,
fill_color = navy,
background_color = "#f0e68c",
grid = true,
region(in1 and in2 , x, -4, 4, y, -4, 4))$
© 2011-2016, TecnoStats.