Tanto en el área de servicios como en la de sistemas de producción, en los que se sirven o fabrican unidades cuyas calidades se describen mediante una variable normal X, interesa comprobar que su media se mantiene próxima al valor nominal μ. Adicionalmente, se debe comprobar que la variabilidad no sea tan grande como para que haya un número apreciable de unidades fuera del intervalo de tolerancia.
El procedimiento para el control de la variabilidad requiere ir tomando pequeñas muestras de tamaño n a intervalos regulares de tiempo. Llamando \(x_{ij}\) a la j-ésima observación de la i-ésima muestra, se calculan la media y la desviación típica de cada una de las muestras: \[ \bar{x}_i = \frac{1}{n} \sum_{j=1}^n x_{ij} \ \ \ \ \ \ \mbox{ y } \ \ \ \ \ \ s_i = \sqrt{\frac{1}{n-1} \sum_{j=1}^n (x_{ij} - \bar{x}_i)^2} \] siendo \(i \in \{1, \ldots, m\}\), con m el número total de muestras realizadas.
Si nos centramos en el control de la variabilidad, disponemos de una secuencia de m cuasidesviaciones típicas \((s_1, s_2, \ldots, s_m)\). Si el proceso se mantiene bajo control, esperamos que estos valores fluctúen alrededor de un valor central no más allá de tres desviaciones típicas; la comprobación de esta hipótesis es el objeto del gráfico de control de las desviaciones.
El valor central buscado es la esperanza de las cuasidesviaciones típicas, cuyo estimador natural es la media de las cuasivarianzas observadas, \[ \bar{s} = \frac{1}{m} \sum_{i=1}^m s_i, \] que es un estimador insesgado de \(\mbox{E}[S]\), ya que \[ \mbox{E}[\bar{S}] = \mbox{E} \left[ \frac{1}{m} \sum_{i=1}^m S_i \right] = \frac{1}{m} \cdot m \cdot \mbox{E}[S_i] = \mbox{E}[S_i], \forall i. \]
Necesitamos ahora conocer y estimar la desviación típica de las \(S_i\). Es bien conocido que la cuasivarianza muestral \(S^2_i\) es un estimador insesgado de la varianza de la población \(\sigma^2\), ya que \[ \frac{(n-1) S^2}{\sigma^2} \sim \chi^2_{n-1}. \] Pero \(S_i\) no es un estimador insesgado de la desviación típica de la población, \(\sigma\); sin embargo, sí es cierto que \[ \frac{\sqrt{n-1} S_i}{\sigma} \sim \chi_{n-1}, \] donde \(\chi_{n-1}\) hace referencia a la distribución con densidad \[ f(x) = \frac{2^{1-\frac{n-1}{2}} x^{n-2} e^{-\frac{x^2}{2}}}{\Gamma\left( \frac{n-1}{2} \right)}, \forall x \geq 0. \]
Es fácil calcular la esperanza de esta distribución con el programa Maxima,
f(x) := 2^(1-(n-1)/2)*x^(n-2)*%e^(-x^2/2) /
gamma((n-1)/2) $
declare(n, integer)$
assume (n>0)$
m1: radcan(integrate(x*f(x),x,0,inf));
\[ {{\sqrt{2}\,\Gamma\left({{n}\over{2}}\right)}\over{\Gamma\left({{n- 1}\over{2}}\right)}} \]
Como consecuencia de lo anterior tenemos que \[ \mbox{E} \left[ \frac{\sqrt{n-1} S_i}{\sigma} \right] = \frac{\sqrt{2} \Gamma\left( \frac{n}{2} \right)}{\Gamma\left( \frac{n-1}{2} \right)}, \] o también, \[ \mbox{E} \left[S_i \right] = \frac{\sqrt{2} \Gamma\left( \frac{n}{2} \right) \sigma}{\sqrt{n-1} \Gamma\left( \frac{n-1}{2} \right)} = c_4 \sigma, \] donde hemos nombrado \(c_4\) al coeficiente de \(\sigma\).
Vamos ahora con la varianza de las \(S_i\). Seguimos utilizando Maxima para calcular el momento de segundo orden,
m2: radcan(integrate(x^2*f(x),x,0,inf)); /* ayudamos a simplificar, haciéndole ver al programa que (n+1)/2=(n-1)/2+1 */ gamma_expand:true$ m2: subst([(n+1)/2=(n-1)/2+1], m2);
\[ n - 1 \]
Finalmente obtenemos la varianza
m2 - m1^2;
\[ -{{2\,\Gamma^2\left({{n}\over{2}}\right)}\over{\Gamma^2\left({{n-1}\over{2}}\right)}}+n-1 \]
Acabamos de demostrar que \[ \mbox{V} \left[ \frac{\sqrt{n-1} S_i}{\sigma} \right] = n-1-{{2\,\Gamma^2\left({{n}\over{2}}\right)}\over{\Gamma^2\left({{n-1}\over{2}}\right)}}, \] o también, \[ \mbox{V} \left[S_i\right] = \left(1-{{2\,\Gamma^2\left({{n}\over{2}}\right)}\over{(n-1) \Gamma^2\left({{n-1}\over{2}}\right)}}\right) \sigma^2 = \left(1-c^2_4 \right) \sigma^2. \]
Recapitulando, el gráfico de control para las desviaciones deberá basarse en la banda \(\bar{s} \mp 3 \cdot \sqrt{1-c^2_4} \, \sigma\), en el que \(\bar{s}\) estima la esperanza de las \(S_i\). En general, desconoceremos la desviación típica de la población, por lo que queda buscarle un buen estimador a \(\sigma\).
Reparamos en el siguiente cálculo: \[ \begin{array}[ccl] \mbox{E} \left[ \frac{\bar{S}}{c_4} \right] & = & \frac{1}{c_4} \mbox{E} \left[ \frac{1}{m} \sum_{i=1}^m S_i\right] \\ & = & \frac{1}{c_4} \cdot \frac{1}{m} \cdot m \cdot \mbox{E} \left[ S_i \right] \\ & = & \frac{1}{c_4} c_4 \sigma \\ & = & \sigma. \end{array} \] Por lo tanto, \(\bar{S}/c_4\) es un estimador insesgado de \(\sigma\).
Así pues, la banda para el gráfico de control del 99% para la desviación típica viene dado por \[ \bar{s} \mp 3 \cdot \sqrt{1-c^2_4} \, \frac{\bar{s}}{c_4}. \]
Ahora es el momento de poner a funcionar todo esto. Partimos de una muestra
m: [[4.8, 5.3, 4.9, 4.9],
[5.0, 4.3, 5.1, 5.6],
[5.9, 5.5, 6.0, 4.6],
[4.3, 5.3, 3.8, 4.8],
[4.8, 6.0, 4.8, 5.0],
[6.0, 4.4, 4.3, 4.6],
[4.8, 6.4, 4.7, 4.9],
[5.1, 4.1, 6.1, 5.5],
[5.3, 5.0, 3.0, 5.0],
[5.3, 4.3, 4.1, 4.3],
[4.4, 6.3, 5.1, 5.8],
[6.8, 4.5, 6.4, 3.7],
[5.7, 5.2, 5.0, 5.3],
[5.6, 5.9, 4.9, 4.2],
[5.0, 4.1, 4.7, 5.4],
[6.2, 4.5, 4.3, 5.2],
[5.6, 5.3, 4.9, 5.7],
[4.6, 5.0, 5.4, 4.9]] $
load(descriptive)$
s: map('std1,m)$
c4: subst([n=length(m[1])], m1/sqrt(n-1)) $
CL: mean(s)$
[UCL,LCL]: CL + 3*sqrt(1-c4^2)*CL/c4*[+1,-1] $
LCL: max(0, LCL) $
vmin: lmin(cons(LCL,s))$
vmax: lmax(cons(UCL,s))$
amp: vmax-vmin$
draw2d(
points_joined = true,
points(s),
yrange = [vmin, vmax] + 0.25*amp*[-1,+1],
/* línea central */
color = red,
points([[0,CL],[length(s),CL]]),
/* extremos de la banda */
line_type = dots,
points([[0,UCL],[length(s),UCL]]),
points([[0,LCL],[length(s),LCL]]) ) $
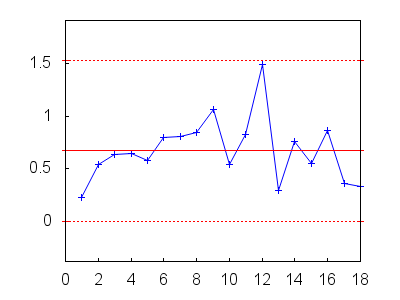
Todo indica que la variabilidad está bajo control. Aún así, convendría investigar bajo qué circunstancias se tomó la muestra número doce, ya que su valor es sensiblemente diferente al resto y sería útil saber si se debió simplemente a una fluctuación aleatoria o a otra causa, como un desajuste temporal del sistema, un operario inexperto, etc.
© 2011-2016, TecnoStats.