
En Maxima, todos los límites se pueden calcular con la función limit. En su versión más sencilla, sólo debemos pasarle la expresión de la función, la variable y el valor hacia el que ésta tiende.
Empezamos por calcular
limx→5x3−7x2+4x−13,
limit(x^3 - 7*x^2 + 4*x - 1/3, x, 5);
−913
Si queremos que la variable tienda hacia ∞, haremos uso del símbolo inf, como en
limx→∞x7−x2+5x9x7−1,
limit((x^7 - x^2+ 5*x)/(9*x^7 - 1), x, inf);
19
Si queremos que la variable tienda hacia −∞, usaremos el símbolo minf. En este ejemplo cambiamos también el nombre de la variable,
limu→−∞eue3u+1,
/* %e es la base de los logaritmos naturales */ limit(%e^u/(%e^(3*u) + 1), u, minf);
0
Veamos qué responde Maxima cuando los límites laterales en un punto no son iguales; nos centramos en el caso
limx→21x−2,
limit(1/(x-2), x, 2);
0
La respuesta que obtenemos, infinity, indica que el límite no converge en x=2. Pero si queremos saber más, podemos calcular los límites laterales por la derecha (plus) y por la izquierda (minus) y obtener con ello
limx→2+1x−2 y limx→2−1x−2,
limit(1/(x-2), x, 2, plus); limit(1/(x-2), x, 2, minus);
∞ −∞
Por último, indicar que el cálculo de límites de sucesiones no difiere en nada del caso de las funciones; por ejemplo, para calcular limnn√5, podemos hacer
limit(5^(1/n), n, inf);
1
Otro ejemplo bien conocido de límite de sucesión,
limn(1+1n)n,
limit((1+1/n)^n, n, inf);
e
Nos planteamos ahora el siguiente problema: calcular b para que se cumpla
limx→∞(x+3x)bx=e.
solve(limit(((x+3)/x)^(b*x), x, inf)= %e, b);
[b=log(√3e13i2−e132),b=log(−√3e13i2−e132),b=13]
Nos da tres soluciones, las dos primeras son complejas y la tercera es un número real.
Calculamos ahora la asíntota oblicua de la función f(x)=sqrt(x+1)2−10. El cálculo lo hacemos en dos pasos; primero obtenemos la pendiente de la asíntota oblicua: m=limx→±∞f(x)x. Si m es un número real distinto de cero, tenemos asíntotas oblicua. Calcularíamos entonces su ordenadas en el origen mediante la expresión n=limx→±∞f(x)−mx.
/* Definimos la función */ y: sqrt((x+1)^2-10) $ /* Calculamos pendientes de posibles asíntotas */ mi: limit(y/x, x, minf) ; md: limit(y/x, x, inf) ;
−1 1
/* Como valen las pendientes, calculamos ordenadas en origen */ oi: limit(y - mi*x, x, minf); od: limit(y - md*x, x, inf);
−1 1
Así, tenemos que la función del ejemplo es asintótica por la derecha a la recta y=x+1 y por la izquierda a la recta y=−x−1.
La función que calcula derivadas en Maxima es diff, que solo necesita de dos argumentos, la expresión de la función a derivar y la variable independiente. Unos ejemplos:
diff( x^2, x); diff( x^n + sin(x), x); diff( exp(cos(u)), u);
2x cosx+nxn−1 −ecosusinu
Las derivadas de mayor orden requieren un tercer argumento a la función diff,
/* derivada de segundo orden */ diff(tan(x) / %e^x, x, 2); /* derivada de tercer orden */ diff(x^2*log(x^3), x, 3);
2e−xsec2xtanx+e−xtanx−2e−xsec2x 6x
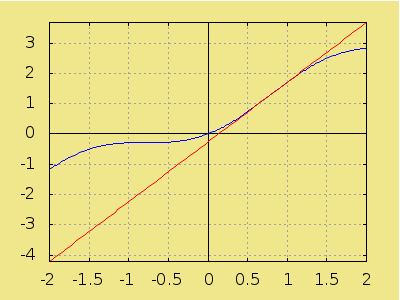
A modo de ejemplo, aplicamos ahora la derivada para representar gráficamente la función f(x)=x+sin2x junto con su recta tangente al punto de abscisa x0=23.
En general, sabemos que la tangente a la función f(x) en el punto de abscisa x0 tiene pendiente igual a f′(x0), siendo f′ la función derivada. La ecuación punto-pendiente toma la forma
y−y0=f′(x0)⋅(x−x0).
/* Definimos la función */ f: x + sin(x)^2$ /* Coordenadas del punto de tangencia */ x0: 2/3 $ y0 : subst(x=x0, f)$ /* Pendiente de la tangente mediante derivada */ m : subst(x=x0, diff(f, x))$ /* Gráfico de la función y su tangente */ load(draw)$ draw2d( grid = true, background_color = "#f0e68c", xaxis = true, yaxis = true, xaxis_type = solid, yaxis_type = solid, explicit(f, x, -2, 2), color = red, explicit(m*(x-x0)+y0, x, -2, 2)) $
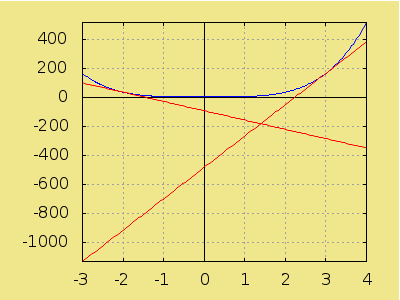
¿En qué punto se cortan la tangentes a la función h(x)=2x4+5 en los puntos de abscisas x0=−2 y x1=3?
/* Definimos la función */ h: 2*x^4 + 5 $ /* Coordenadas de los puntos de tangencia. */ (x0: -2, y0: subst(x=x0, h), [x0, y0]) $ (x1: 3, y1: subst(x=x1, h), [x1, y1]) $ /* Derivada de la función */ dh: diff(h, x) $ /* Pendientes de cada una de las tangentes */ m0: subst(x= x0, dh) $ m1: subst(x= x1, dh) $ /* Resolvemos el sistema formado por las dos rectas */ solve([y = m0*(x-x0)+y0, y = m1*(x-x1)+y1], [x, y]);
[[x=3928,y=−12617]]
/* Dibujamos función y tangentes */ load(draw) $ draw2d( grid = true, background_color = "#f0e68c", xaxis = true, yaxis = true, xaxis_type = solid, yaxis_type = solid, explicit(h, x, -3, 4), color = red, explicit(m0*(x-x0)+y0, x, -3, 4), explicit(m1*(x-x1)+y1, x, -3, 4)) $
El cálculo de la primitiva de una función se hace en Maxima con la función integrate.
integrate(x^3 - 2/3*x^2 - x + 1/4, x);
x44−2x39−x22+x4
La función integrate no devuelve la constante de integración porque en la mayoría de las situaciones no es necesario tenerla en cuenta.
Maxima dispone de un mecanismo de inhibición de cálculo consistente en hacer preceder la expresión que no se quiere evaluar con la comilla simple ('); de esta manera podemos interpretar más fácilmente los resultados,
'integrate(sin(x)^2, x) = integrate(sin(x)^2, x) + k;
∫sin2xdx=x−sin(2x)22+k
La integral definida se calcula añadiendo dos argumentos más a la función integrate, indicando los límites de integración. Procedemos con el cálculo de ∫32xsin2xdx
integrate(x*sin(x)^2, x, 2, 3);
4sin4+cos4−88−6sin6+cos6−188
© 2011-2016, TecnoStats.