Graphical representation of complex numbers

The binomial form of a complex number is \(a + b i\), where a is the real part, b is the imaginary part, and \(i=\sqrt{-1}\) is the imaginary unit, which is represented in Maxima as %i.

We store in variable u the complex number \(5-3i\),

u: 5-3*%i; 

\[ 5-3\,i \]

now we obtain the real part,

realpart(u);

\[ 5 \]

and the imaginary part,

imagpart(u); 

\[ -3 \]

If the real and imaginary parts are interpreted as the coordinates of a point on the Euclidean plane, we can represent the complex number graphically. In order to do so, let's define function argand,

load("draw")$
ratprint : false $

argand(z) :=
  block([x,y,r,fr,a,fa,fpprintprec: 3],
    x: realpart(z),
    y: imagpart(z),
    r: abs(z),
    fr: float(r),
    a: carg(z),
    fa: float(a*180/%pi),
    draw2d(
      terminal          = png,
      dimensions        = [400,400],
      grid              = true,
      proportional_axes = xy,
      xaxis             = true,
      yaxis             = true,
      xaxis_type        = solid,
      yaxis_type        = solid,
      xrange            = [min(-0.2*fr, 1.3*min(0,x)),
                           max(0.2*fr,1.3*max(0,x))],
      yrange            = [min(-0.2*fr, 1.3*min(0,y)),
                           max(0.2*fr,1.3*max(0,y))],
      points_joined     = true,
      points([[0,0],[x, y]]),
      color             = black,
      ellipse(0, 0, 0.1*fr, 0.1*fr, 0, fa),
      point_type        = 'filled_circle,
      point_size        = 2,
      points([[x,y]]),
      label([concat("(",float(x),",",float(y),")"), 1.2*x, 1.2*y],
            [sconcat("arg=",carg(z)), 0.15*fr*cos(a/2), 0.15*fr*sin(a/2)],
            [sconcat("m=",abs(z)), 0.5*fr*cos(0.9*a), 0.5*fr*sin(a)])) ) $

Now we proceed with the graphical representation of our complex number,

argand(u) $

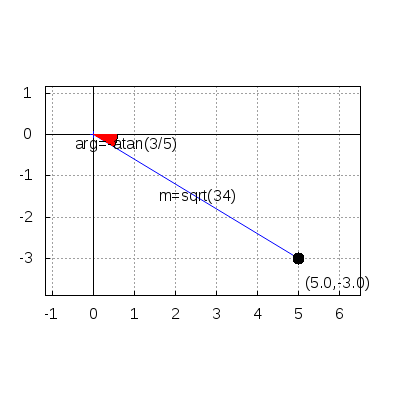
The resulting plot also shows the argument of the complex number,

carg(u);

\[ -\arctan \left({{3}\over{5}}\right) \]

and its module,

abs(u);

\[ \sqrt{34} \]

These two quantities give rise to the polar form of the complex number,

polarform(u); 

\[ \sqrt{34}\,e^ {- i\,\arctan \left({{3}\over{5}}\right) } \]

This is the representation of complex number \(\sqrt{2}\,e^{{{i\,\pi}\over{4}}}\), which is in polar form,

v: sqrt(2)*%e^((%i*%pi)/4) $
argand(v) $

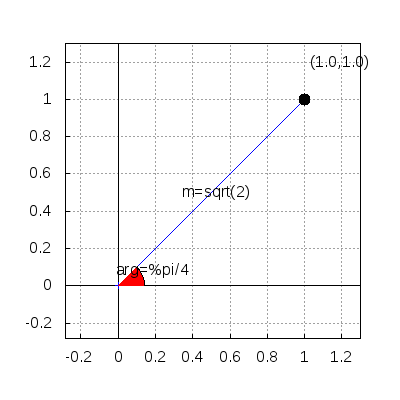
The same number in binomial form,

rectform(v); 

\[ i+1 \]

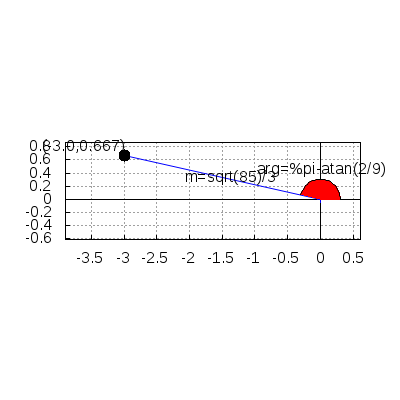
Some other examples in binomial form:

argand(-3+2/3*%i) $ 

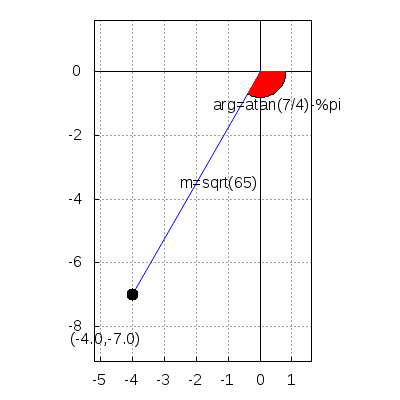
argand(-4-7*%i) $

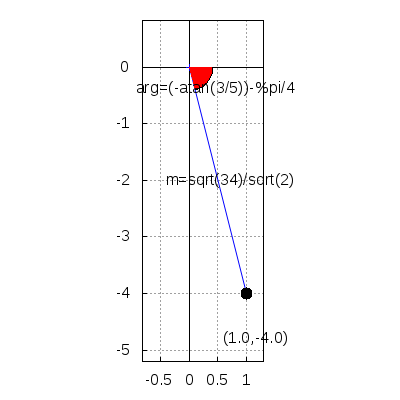
Finally, the quotient of u and v,

q: u/v $
rectform(q);

\[ 1-4\,i \]

argand(q) $

© 2011-2016, TecnoStats.