Los problemas de programación lineal entran dentro del grupo de problemas de optimización, en los que hay que decidir qué valores hay que dar a ciertas variables, bien para que maximicen un beneficio, bien para que minimicen un riesgo o coste económico.
Los problemas de PL que solo involucren dos variables pueden resolverse gráficamente.
Trataremos la situación con un ejemplo.
Un granjero tiene 480 Ha en las que puede sembrar trigo o maíz. Él estima que puede trabajar hasta 800 horas dentro del período de siembra. Sabe que cada Ha de trigo le reporta un beneficio de 30€ y que cada Ha de Maíz sembrada le aportará un beneficio de 40€. El tiempo de trabajo para cada Ha depende de la especie; así, cada Ha de trigo le ocupa 1h de trabajo y cada Ha de maíz requiere a su vez de 2h. Se pregunta:
Llamaremos t al número de Ha dedicadas a trigo y m al maíz. Sean cuales sean los valores de estas dos variables, su beneficio será:
beneficio : 30 * t + 40 * m;
\[ 30\,t+40\,m \]
En primer lugar, debemos considerar que tanto la superficie dedicada al trigo como la dedicada al maíz deben ser cantidades no negativas. Así tenemos,
restriccion1 : t >= 0 $ restriccion2 : m >= 0 $
Las horas de trabajo no pueden exceder de 800 h, luego
restriccion3 : 1 * t + 2 * m <= 800 $
En primer lugar, queremos representar gráficamente la zona del plano que cumple estas tres restricciones. Para ello definimos una función que podremos utilizar luego tantas veces como queramos,
load(draw) $
set_draw_defaults(
xaxis = true,
yaxis = true,
xaxis_type = solid,
yaxis_type = solid,
grid = true,
x_voxel = 50,
y_voxel = 50,
dimensions = [400, 400],
background_color = "#f0e68c" )$
rnd_color():=
block([obase : 16, col : "#"],
for i : 1 thru 6 do
col : concat(col,
block([sz : concat(random(16))],
substring(sz, slength(sz)))),
col)$
region_factible(restricciones,
var1, var1min, var1max,
var2, var2min, var2max) :=
block([ecu],
ecu:delete([], makelist(solve(lhs(k) = rhs(k), var2),
k, restricciones)),
cons(
region(apply("and", restricciones),
var1, var1min, var1max,
var2, var2min, var2max) ,
map(
lambda([ec],
[color = rnd_color(),
key = string(ec),
explicit(rhs(first(ec)),var1,var1min,var1max)] ),
ecu)) )$
recta(benef, valor, var, varmin, varmax, var2) :=
[color = black,
key = "",
line_width = 3,
explicit(rhs(first(solve(valor = benef, var2))),
var, varmin, varmax)] $
Ahora ejecutamos la función con las restricciones de nuestro problema,
draw2d(
region_factible(
[restriccion1, restriccion2, restriccion3],
t, -10, 800, m, -10, 500))$
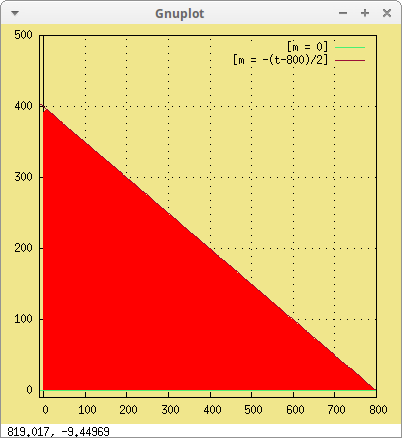
Las restricciones 1 y 2 provocan que la región se encuentre en el primer cuadrante del plano. El lado inclinado del triángulo es la recta que se obtiene cuando en la restricción 3 sustituimos la desigualdad por la igualdad.
Pero hay otra restricción más; el número total de Ha a sembrar no puede exceder de 480,
restriccion4 : t + m <= 480 $
Veamos qué puntos del plano verifican las restricciones 1, 2 y 4 (la 3 todavía no),
draw2d(
region_factible(
[restriccion1, restriccion2, restriccion4],
t, -10, 800, m, -10, 500))$
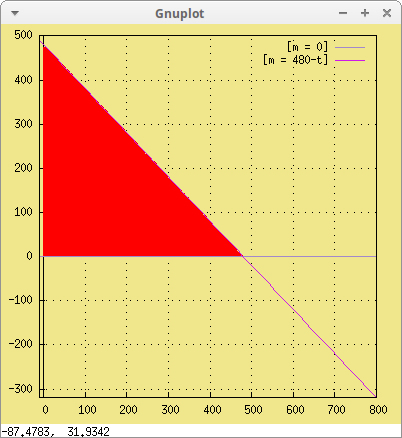
El conjunto de pares (t, m) que cumplen todas las condiciones anteriores forman lo que se conoce como región factible del problema de la programación lineal. Se obtiene dibujando la intersección de todas las regiones anteriores,
draw2d(
region_factible(
[restriccion1, restriccion2, restriccion3, restriccion4],
t, -10, 800, m, -10, 500))$
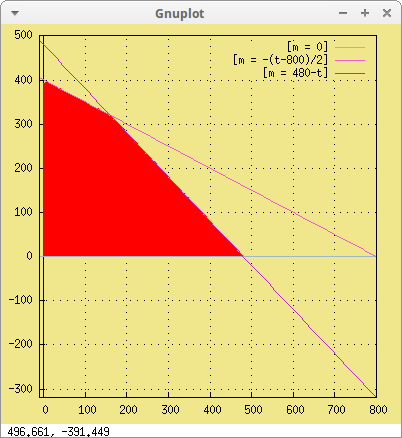
Si el granjero opta por dedicar 200 Ha al trigo y 100 Ha al maíz su beneficio será:
subst([t = 200, m = 100], beneficio);
\[ 10000 \]
Si decide hacer t = 100 y m = 300, el beneficio será:
subst([t = 100, m = 300], beneficio);
\[ 15000 \]
La pregunta que queda por resolver es: ¿Cuántas hectáreas debe asignar a cada especie de cereal para obtener el máximo beneficio? No se debe olvidar que los valores (t, m) hay que seleccionarlos dentro la región factible.
Vamos a escoger un beneficio a priori y observar qué valores del par (t, m) lo pueden generar. Empezamos por un beneficio de 5000€,
draw2d(
yrange = [-100, 500],
region_factible(
[restriccion1, restriccion2, restriccion3, restriccion4],
t, -10, 500, m, -10, 500),
recta(beneficio, 5000, t, -10, 500, m) )$
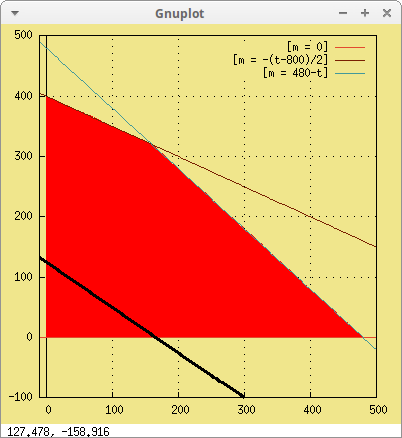
Todos los puntos de la recta que coinciden sobre la región factible aportan un beneficio de 5000€.
Ahora añadimos las soluciones que aportan un beneficio de 0€ y un beneficio de 10000€,
draw2d(
yrange = [-100, 500],
region_factible(
[restriccion1, restriccion2, restriccion3, restriccion4],
t, -10, 500, m, -10, 500),
recta(beneficio, 0, t, -10, 500, m),
recta(beneficio, 5000, t, -10, 500, m),
recta(beneficio, 10000, t, -10, 500, m) )$
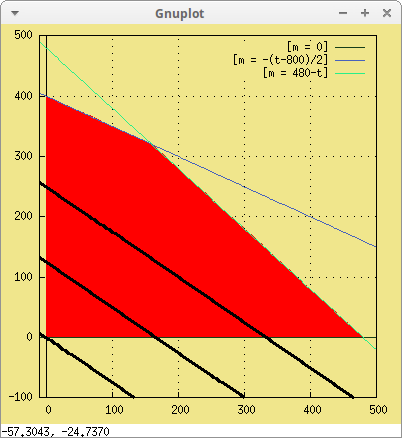
Es obvio que para obtener 0€, la solución se reduce a quedarse en casa en lugar de ir a trabajar: t=0, m=0.
También se observa que para obtener mayores beneficios, las soluciones siempre se encuentran sobre rectas paralelas cuyas ordenadas en el origen están cada vez más arriba.
Añadimos las soluciones para obtener beneficios de 15000€ y 17000€.
draw2d(
yrange = [-100, 500],
region_factible(
[restriccion1, restriccion2, restriccion3, restriccion4],
t, -10, 500, m, -10, 500),
recta(beneficio, 0, t, -10, 500, m),
recta(beneficio, 5000, t, -10, 500, m),
recta(beneficio, 10000, t, -10, 500, m),
recta(beneficio, 15000, t, -10, 500, m),
recta(beneficio, 17000, t, -10, 500, m) )$
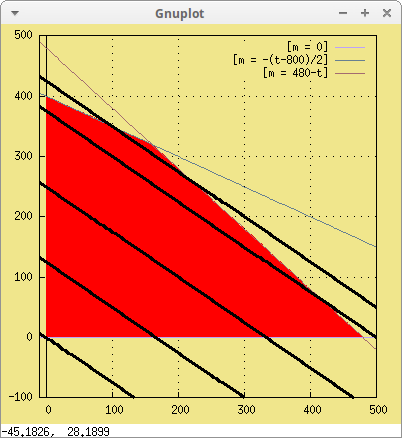
Nos estamos acercando a los límites de la región factible, pero claramente nos imaginamos que el último punto que va a tocar la serie de rectas paralelas es la intersección de las dos rectas asociadas a las restricciones 3 y 4,
recta3: lhs(restriccion3) = rhs(restriccion3);
\[ t+2\,m=800 \]
y
recta4: lhs(restriccion4) = rhs(restriccion4);
\[ t+m=480 \]
Ambas rectas se cortan en
solucion: solve([recta3, recta4], [t,m]);
\[ \left[ \left[ t=160 , m=320 \right] \right] \]
Luego el granjero debe dedicar 160Ha al trigo y 320Ha al maíz. El beneficio obtenido es:
optimo: subst(first(solucion), beneficio);
\[ 17600 \]
Para verlo, volvemos a dibujar la región factible y la recta paralela asociada al benefico máximo:
draw2d(
yrange = [-100, 500],
region_factible(
[restriccion1, restriccion2, restriccion3, restriccion4],
t, -10, 500, m, -10, 500),
recta(beneficio, optimo, t, -10, 500, m))$
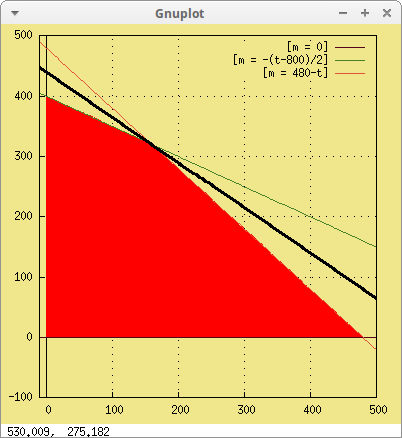
El problema. Una empresa fabrica tres productos, P1, P2 y P3, en dos plantas, A y B. La planta A produce diariamente 1.000 unidades de P1, 3.000 unidades de P2 y 5.000 de P3. La planta B produce diariamente 2.000 unidades de cada uno de los tres productos. La empresa se ha comprometido a entregar a sus clientes, al menos, 80.000 unidades de P1, 160.000 de P2 y 200.000 de P3. Sabiendo que el coste diario de producción es de 1200€. en cada planta, ¿cuántos días debe trabajar cada planta para que se cubran los objetivos comprometidos con el mínimo coste?
Llamaremos a a los días de trabajo de A y b a los días de B.
Coste de producción:
coste: 1200 * a + 1200 * b;
\[ 1200\,b+1200\,a \]
Las restricciones son:
restriccion1 : a >= 0 $ restriccion2 : b >= 0 $ /* restricción asociada al producto P1 */ restriccion3 : 1000 * a + 2000 * b >= 80000 $ /* restricción asociada al producto P2 */ restriccion4 : 3000 * a + 2000 * b >= 160000 $ /* restricción asociada al producto P3 */ restriccion5 : 5000 * a + 2000 * b >= 200000 $
Dibujamos la región factible,
draw2d(
yrange = [-10, 100],
region_factible(
[restriccion1, restriccion2, restriccion3, restriccion4, restriccion5],
a, -10, 100, b, -10, 100))$
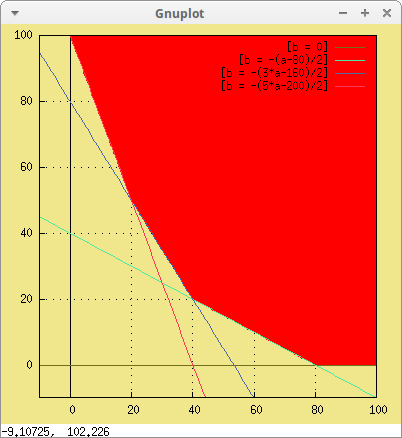
Vamos dibujando algunas rectas de costes para ir viendo dónde estará la solución del problema,
draw2d(
yrange = [-10, 100],
region_factible(
[restriccion1, restriccion2, restriccion3, restriccion4, restriccion5],
a, -10, 100, b, -10, 100),
recta(coste, 0, a, -10, 100, b),
recta(coste, 42000, a, -10, 100, b),
recta(coste, 60000, a, -10, 100, b),
recta(coste, 90000, a, -10, 100, b),
recta(coste, 120000, a, -10, 100, b))$
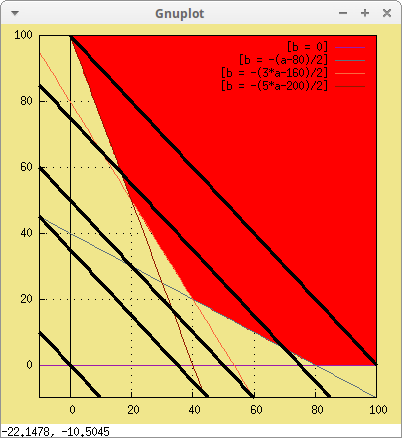
Nos imaginamos que la recta paralela de mínimo coste debe pasar por la intersección de las restricciones 3 y 4. Procedemos entonces a calcular su intersección,
recta3: lhs(restriccion3) = rhs(restriccion3)$ recta4: lhs(restriccion4) = rhs(restriccion4)$ solucion: solve([recta3, recta4], [a,b]);
\[ \left[ \left[ a=40 , b=20 \right] \right] \]
El valor mínimo alcanzado es, pues,
optimo: subst(first(solucion), coste);
\[ 72000 \]
La conclusión es la siguiente: el coste mínimo de producción se obtiene cuando la factoría A opera 40 días y la B 20. El coste mínimo es de 72000€.
draw2d(
yrange = [-10, 100],
region_factible(
[restriccion1, restriccion2, restriccion3, restriccion4, restriccion5],
a, -10, 100, b, -10, 100),
recta(coste, 72000, a, -10, 100, b))$
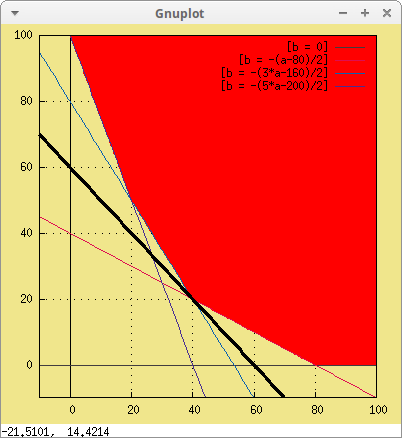
Los problemas que hemos resuelto hasta aquí solo tenían dos variables y se pueden resolver gráficamente siguiendo el método descrito. Si en lugar de dos, tuviésemos un problema de tres variables, en lugar de dibujar figuras en un plano, tendríamos que hacerlo en el espacio, y la cosa se complicaría bastante. Y aún peor, los problemas reales, que se presentan en la organización de empresas y en la industria, fácilmente alcanzan decenas o centenas de variables y restricciones.
El algoritmo Simplex lo ideó durante la Segunda Guerra Mundial George Bernard Dantzig (1914-2005) y se aplicó para mejorar la organización del abastecimiento de las tropas aliadas. Con este algoritmo se mejoraron los tiempos de entrega de víveres y repuestos de armamento, evitando que se deteriorasen en los almacenes esperando el momento de ser enviados al frente.
Nos planteamos el problema de maximizar la función objetivo \[ F(x_1,x_2,x_3) = 2 x_1 + 4 x_2 + x_3 + x_4 \] sujeta a las siguientes condiciones: \[ \left\{ \begin{array}{lcl} x_1 + 3 x_2 + x_4 & \leq & 4 \\ 2 x_1 + x_2 & \leq & 3 \\ x_2 + 4 x_3 + x_4 & \leq & 3 \end{array} \right. \]
Cargamos en memoria el paquete simplex y ejecutamos la función maximize_lp.
load("simplex")$
/* Función objetivo */
F : 2*x1 + 4*x2 + x3 + x4 $
/* Restricciones */
r1 : x1 + 3*x2 + x4 <= 4 $
r2 : 2*x1 + x2 <= 3 $
r3 : x2 + 4*x3 + x4 <= 3 $
r4 : x1 >= 0 $
r5 : x2 >= 0 $
r6 : x3 >= 0 $
r7 : x4 >= 0 $
/* Resolución del problema de PL */
maximize_lp(F, [r1, r2, r3, r4, r5, r6, r7]);
\[ \left[ {{13}\over{2}} , \left[ {\it x_3}={{1}\over{2}} , {\it x_4}= 0 , {\it x_2}=1 , {\it x_1}=1 \right] \right] \]
El resultado anterior lo interpretamos de la siguiente manera: el valor máximo es \(\frac{13}{2}\), que se obtiene cuando \(x_1=1, x_2=1, x_3=\frac{1}{2}, x_4=0\).
Resolvemos ahora el siquiente problema de minimización: \[ \mbox{Min. } F(x_1,x_2,x_3) = 2 x_1 + 5 x_2 + 10 x_3 + 7 x_4 \\ \mbox{Sujeto a } \left\{ \begin{array}{lcl} 4 x_1 + 2 x_2 + 10 x_3 + 3 x_4 & \leq & 100 \\ x_1 + 3 x_3 + 2 x_4 & \leq & 60 \\ 8 x_1 + x_2 + x_3 + 3 x_4 & \leq & 40 \\ x_1, x_2, x_3, x_4 & \geq & 0 \end{array} \right. \]
/* Función objetivo */ obj : 2*x1 + 5*x2 + 10*x3 + 7*x4 $ /* Restricciones */ r1 : 4*x1 + 2*x2 + 10*x3 + 3*x4 >= 100 $ r2 : x1 + 3*x3 + 2*x4 <= 60 $ r3 : 8*x1 + x2 + x3 + 3*x4 <= 40 $ r4 : x1 >= 0 $ r5 : x2 >= 0 $ r6 : x3 >= 0 $ r7 : x4 >= 0 $ /* Resolución del problema de PL */ minimize_lp(obj, [r1, r2, r3, r4, r5, r6, r7]);
\[ \left[ {{1750}\over{19}} , \left[ {\it x_4}=0 , {\it x_3}={{160 }\over{19}} , {\it x_2}=0 , {\it x_1}={{75}\over{19}} \right] \right] \]
© 2011-2016, TecnoStats.