En Maxima se representa la unidad imaginaria \(i=\sqrt{-1}\) como %i. El número complejo \(3+4 i\) se representa como
z: 3+4*%i;
\[4\,i+3\]
Sabemos que cualquier número complejo \(z\) tiene \(n\) raíces \(n\)-ésimas. Hacemos \(n=5\) y procedemos
n: 5 $ m: cabs(z)^(1/n) $ r: m*exp(%i*makelist((carg(z)+k*2*%pi)/n,k,0,n-1));
\[\left[ 5^{{{1}\over{5}}}\,e^{{{i\,\arctan \left({{4}\over{3}} \right)}\over{5}}} , 5^{{{1}\over{5}}}\,e^{{{i\,\left(\arctan \left( {{4}\over{3}}\right)+2\,\pi\right)}\over{5}}} , 5^{{{1}\over{5}}}\,e ^{{{i\,\left(\arctan \left({{4}\over{3}}\right)+4\,\pi\right)}\over{ 5}}} , \\ 5^{{{1}\over{5}}}\,e^{{{i\,\arctan \left({{4}\over{3}}\right) }\over{5}}-{{4\,i\,\pi}\over{5}}} , 5^{{{1}\over{5}}}\,e^{{{i\, \arctan \left({{4}\over{3}}\right)}\over{5}}-{{2\,i\,\pi}\over{5}}} \right]\]
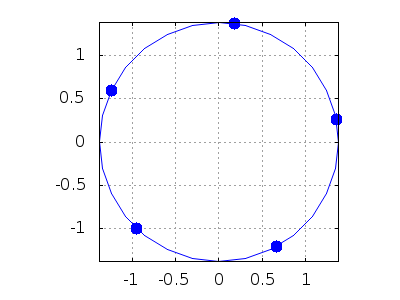
Representamos gráficamente las cinco raíces,
draw2d(
proportional_axes = xy,
grid = true,
point_size = 2,
point_type = filled_circle,
parametric(m*cos(t),m*sin(t),t,0,2*%pi),
points(realpart(r),imagpart(r)) ) $
© 2011-2016, TecnoStats.