Recordamos que una función \(f: D \mapsto R\), con \(D \subset R\), infinitamente diferenciable en un entorno del punto \(a \in D\), puede expresarse del siguiente modo: \[ f(x)= f(a) + \frac{f'(a)}{1!} (x-a) + \frac{f''(a)}{2!} (x-a)^2 + \frac{f^{(3)}(a)}{3!} (x-a)^3 + \ldots \]
La expresión anterior es el polinomio de Taylor; nosotros debemos elegir cuántos términos utilizamos en la aproximación. A mayor grado del polinomio, más fiel será la aproximación polinómica en el entorno de \(a\).
La función que definimos a continuación nos representará tanto la función como el polinomio de Taylor, gráfica y simbólicamente.
fpprintprec: 4 $
ptaylor(f,n,x0,r):=
block([xmin,xmax,pt],
[xmin,xmax]: float([x0-r, x0+r]),
if not listofvars(f) = [x] or
not numberp(xmax) or
not integerp(n) or
n <= 0
then out("Entrada incorrecta")
else ( pt: float(factor(taylor(f, 'x, x0, n))),
draw2d(
key = "Polinomio de Taylor, p(x)",
color = cyan,
explicit(pt,'x,xmin,xmax),
key = "f(x)",
color = blue,
explicit(f,x,xmin,xmax),
key = "g(x)",
grid = true,
xaxis = true,
xaxis_type = solid,
yaxis = true,
yaxis_type = solid),
expand(pt)));
La función ptaylor recién programada necesita cuatro argumentos: la expresión simbólica de la función con variable independiente x, el grado del polinomio de Taylor, el punto alrededor del cual se hace la aproximación y el radio del entorno para la representación gráfica.
Empezamos con el polinomio de grado uno en el punto de abscisa \(x=1\), que no es otro que la recta tangente en ese punto,
ptaylor(sin(x^2), 1, %pi/3, 1) ;
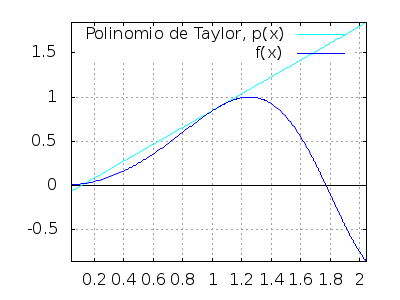
\[0.96\,x-0.11\]
Aproximación de grado dos,
ptaylor(sin(x^2), 2, %pi/3, 1) ;
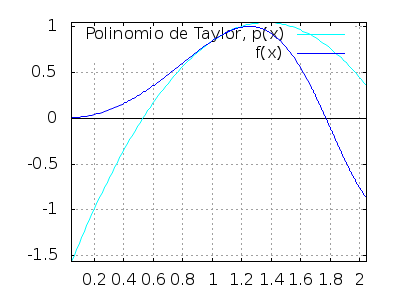
\[-1.495\,x^2+4.087\,x-1.751\]
Aproximación de grado tres,
ptaylor(sin(x^2), 3, %pi/3, 1) $
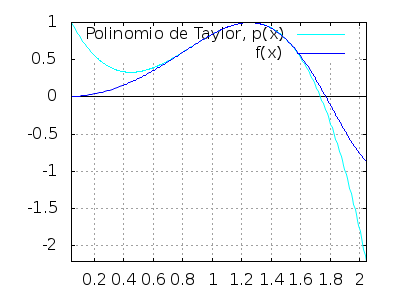
\[-2.562\,x^3+6.556\,x^2-4.343\,x+1.192\]
© 2011-2016, TecnoStats.