
Once you have opened a Maxima session, load package draw and then set global variable draw_renderer to vtk:
load("draw") $
draw_renderer: 'vtk $
To read the documentation on object elevation_grid, write the following sentence:
describe(elevation_grid) $
A random matrix:
m: apply(matrix, makelist(makelist(random(1.0),k,1,10),i,1,10)) $ draw3d( color = white, elevation_grid(m, 0, 0, 10, 10)) $
Local option wired_surface on an elevation_grid object:
m: apply(
matrix,
makelist(makelist(random(1.0),k,1,10),i,1,10)) $
draw3d(
enhanced3d = true,
wired_surface = true,
elevation_grid(m,0,0,3,2)) $

Modules:
m: apply(
matrix,
makelist(makelist(mod(k,i),k,1,20),i,1,20)) $
draw3d(
enhanced3d = true,
elevation_grid(m, 0, 0, 20, 20)) $

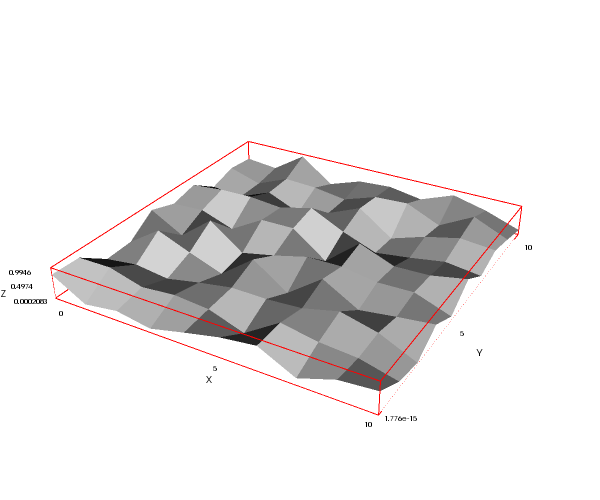
An artificial landscape. The simulation may take a while, be patient:
terrain_generator(m) :=
block([terra: float(zeromatrix(m,m)), iter:100, x, y, slope],
for k:1 thru iter do(
[x, y]: 1 + [random(m), random(m)],
slope: tan(random(180.0)),
for i:1 thru m do
for j:1 thru m do
if i < slope * (j-x) + y
then terra[i,j]: terra[i,j] + iter/k
else terra[i,j]: terra[i,j] - iter/k ) ,
terra / iter) $
terreno: terrain_generator(100)$
draw3d(
enhanced3d = true,
palette = gray,
elevation_grid(terreno, 0, 0, 10, 10)) $

Lena. We read a list of 40000 gray levels and transform it in a square matrix of order 200:
m1: read_list("lena.txt")$
lena: apply(matrix, makelist(makelist(m1[j],j,k*200+1, k*200+200),k,0,199)) $
draw3d(
palette = gray,
enhanced3d = true,
elevation_grid(lena/10.0,1,1,100,100)) $

2D Fast Fourier Transform. Contributed by Edward G. Montague (thanks):
/* Load FFT package */
load(fft)$
N:128$
M:128$
/* 2d fft
input array a2
output array b2 */
fft2(a2,b2):=
block(
local(i,j,n,m,ab),
ab: arrayinfo(a2),
n: ab[3][1],
m: ab[3][2],
n: n+1,
m: m+1,
array(b1, float, n-1),
fillarray(b1, [0.0]),
for j:0 thru m-1 do (
for i:0 thru n-1 do
b1[i]: a2[i,j],
bb: listarray(b1),
cc: fft(bb),
for i:0 thru n-1 do
b2[i,j]: cc[i+1]),
kill(b1,cc,i,j),
array(b1,float,m-1),
fillarray(b1,[0.0]),
for i:0 thru n-1 do (
for j:0 thru m-1 do
b1[j]: b2[i,j],
bb: listarray(b1),
cc: fft(bb),
for j:0 thru m-1 do
b2[i,j]:cc[j+1]),
b2 )$
/* Exchange 2d array values for centered spectrum .
Input array b2
Output array c2*/
vxchg(b2,c2) :=
block(
local(i,j,n,m,i1,j1,ab),
ab: arrayinfo(b2),
n: ab[3][1],
m: ab[3][2],
n: n+1,
m: m+1,
array(b1,float,m-1),
array(x2,float,m-1),
fillarray(b1,[0.0]),
fillarray(x2,[0.0]),
xb: listarray(x2),
for i:0 thru n-1 do (
for j:0 thru m-1 do
b1[j]: b2[i,j],
bb: listarray(b1),
for j:1 thru m/2 do (
i1: j+(m/2),
xb[j]: bb[i1],
xb[i1]: bb[j]),
for j:0 thru m-1 do
c2[i,j]:xb[j+1]),
kill(b1,bb,cc,x2,xb,i,j),
array(b1,float,n-1),
fillarray(b1,[0.0]),
array(x2,float,n-1),
fillarray(x2,[0.0]),
xb: listarray(x2),
for j:0 thru m-1 do(
for i:0 thru n-1 do
b1[i]:c2[i,j],
bb:listarray(b1),
for i:1 thru n/2 do (
j1: i+(n/2),
xb[i]: bb[j1],
xb[j1]: bb[i] ),
for i:0 thru n-1 do
c2[i,j]:xb[i+1]),
c2 )$
/* Dimension arrays and generate data */
array(a2,float,N-1,M-1)$
array(b2,float,N-1,M-1)$
array(c2,float,N-1,M-1)$
fillarray(a2,[0.0])$
fillarray(b2,[0.0])$
fillarray(c2,[0.0])$
for j:0 thru (M/4)-1 do
for i:0 thru (N/8)-1 do
a2[i,j]: 1 $
/* Generate 2d matrix from 2d array .
Input array a2
Output matrix Mat1 */
Mat1: genmatrix(a2,N-1,M-1)$
/* 2d fft
Input array a2
Output array b2 */
b2: fft2(a2,b2)$
/* Absolute value of 2d array b2.
Input array b2
Output array b2 */
for i:0 thru N-1 do
for j:0 thru M-1 do
b2[i,j]: abs(b2[i,j]) $
/* Exchange values.
Input array b2
Output array c2 */
c2: vxchg(b2,c2)$
/* Generate 2d matrix from 2d array.
Input array c2
Output matrix Mat2 */
Mat2: genmatrix(c2,N-1,M-1)$
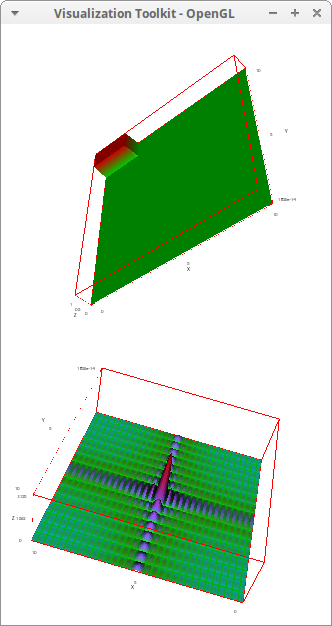
/* Draw the two matrices */
set_draw_defaults(
enhanced3d = [log(10000*z+1)/log(10001), x, y, z],
palette = [4,-10,17])$
draw(
dimensions = [800, 400],
columns = 1,
/* Draw 2d matrix , Mat1, with logarithmic colouring.
This is the 2d function data. */
gr3d(elevation_grid(Mat1, 0, 0, 10, 10)),
/* Draw 2d matrix, Mat2, with logarithmic colouring.
This is the centered spectrum */
gr3d(elevation_grid(100*Mat2, 0, 0, 10, 10)) )$
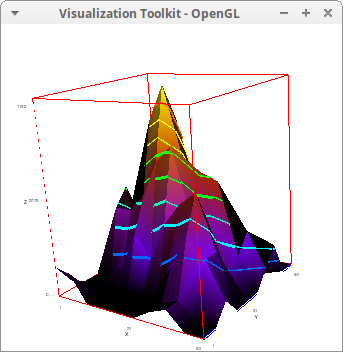
Isolines on an elevation_grid surface.
m: matrix(
[ 0.0, 0.0, 9.5,21.0, 10.5, 0.0, 0.0, 0.0, 0.0, 0.0],
[ 0.0, 2.1, 2.1, 0.0, 52.5,10.5, 6.3, 0.0, 0.0, 0.0],
[ 0.0, 2.1, 9.5,10.5, 63.0,21.0,27.3,10.5, 0.0,21.0],
[ 0.0, 0.0, 9.5,42.0, 94.5,52.5,33.6,21.0,31.5,10.5],
[21.0,52.5, 6.0,94.5,115.5,73.5,67.2,63.0,21.0, 0.0],
[10.5,42.0,42.0,52.5, 73.5,84.0,42.0,42.0,10.5, 0.0],
[ 0.0, 0.0,10.5,31.5, 21.0,42.0,54.6,63.0,31.5, 0.0],
[ 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,23.1,42.0,31.5,10.5],
[ 5.3, 3.0, 0.0, 0.0, 0.0, 0.0, 6.3,10.5, 0.0, 0.0],
[18.2,16.4, 0.0, 0.0, 0.0, 0.0, 6.3,10.5, 0.0, 0.0]) $
draw3d(
enhanced3d = [z,x,y,z],
isolines = [x-y*z,x,y,z],
line_width = 3,
elevation_grid(m,1,1,100,100)) $
Another example of an elevation_grid surface. This time, we read a list of 8100 heights and transform it in a square matrix of order 90.
m2: read_list("terrain.txt")$
terr: apply(matrix, makelist(makelist(m2[j],j,k*90+1, k*90+90),k,0,89)) $
draw3d(
enhanced3d = [z,x,y,z],
isolines = [z,x,y,z],
line_width = 2,
elevation_grid(terr,1,1,100,100)) $

The Mandelbrot set as an elevation grid. A kind contribution from Edward Montague.
MandelB(c,niter):=block([n:0,z:0],
while ((abs(z) < 4) and (n < niter)) do (
z:z*z+c,
z:expand(z),
n:n+1 ),
n )$
compile(MandelB)$
nd:200$
x1:-2.5$
y1:-1.5$
x2:1.5$
y2:1.5$
dx:(x2-x1)/nd$
dy:(y2-y1)/nd$
declare(u,complex)$
declare(niter,integer)$
declare(i,integer)$
declare(j,integer)$
declare(m,integer)$
a1:zeromatrix(nd+1,nd+1)$
niter:80$
j:1$
for y:y1 thru y2 step dy do(
i:1,
for x:x1 thru x2 step dx do (
c:x+%i*y,
m:MandelB(c,niter),
a1[i,j]:m,
i:i+1 ),
j:j+1 )$
load("draw") $
draw_renderer: 'vtk $
draw3d(
enhanced3d = true,
elevation_grid(a1*0.4, 1, 1, nd, nd)) $

This is another example of a 3D fractal, a contribution by Tomio Arisaka. This example also shows how to integrate a user defined Lisp function stored in an external file, mandelbrot-julia.lisp, into a Maxima session. The Javascript code for the interactive visualization is based on the ThreeJS library.
The elevation-grid object is exported to the ply format by means of the terminal option.
load("./mandelbrot-julia.lisp") $
/* example of Julia set */
scale : 120.0 $
iteration : 40 $
[x0, y0] : [0.3090169943749475, -0.535233134659635] $
[x1, x2, y1, y2] : [-1.2, 1.2, -1.4, 1.4] $
width : abs (x2 - x1);
hight : abs (y2 - y1);
size_x : round (width * scale);
size_y : round (hight * scale);
ma1 : zeromatrix (size_y, size_x) $
?julia\-set1 (ma1, iteration, x0, y0, x1, x2, y1, y2);
draw3d(
terminal = ply,
enhanced3d = true,
palette = [10, 17, 10],
elevation_grid(ma1*float(1/(iteration*2*2)), x1, y1, width, hight)) $
The necessary Javascript code looks as follows:
<div id="ThreeJS"></div>
<script>
var container, scene, camera, renderer, controls, sky;
init();
animate();
function init() {
scene = new THREE.Scene();
var width = screen.width;
height = screen.height;
camera = new THREE.PerspectiveCamera(50, width / height, 1, 20000);
camera.position.set(2,2,2);
scene.add(camera);
renderer = new THREE.WebGLRenderer();
renderer.setSize(width, height);
container = document.getElementById( 'ThreeJS' );
container.appendChild( renderer.domElement );
controls = new THREE.TrackballControls(camera, renderer.domElement);
controls.rotateSpeed = 5.0;
var light = new THREE.PointLight(0xffffff);
light.position.set(100,250,100);
scene.add(light);
var light = new THREE.PointLight(0xffffff);
light.position.set(-200,-150,-300);
scene.add(light);
var skyBoxGeometry = new THREE.CubeGeometry( 10000, 10000, 10000 );
var skyBoxMaterial = new THREE.MeshBasicMaterial({color: 0xccccff,
side: THREE.BackSide});
sky = new THREE.Mesh( skyBoxGeometry, skyBoxMaterial );
scene.add(sky);
var loader = new THREE.PLYLoader();
loader.load( 'maxima_out.ply',
function ( geometry ) {
geometry.computeFaceNormals();
var material = new THREE.MeshPhongMaterial( {
color: 0xff5533,
specular: 0x111111,
shininess: 200,
side: THREE.DoubleSide } );
var mesh = new THREE.Mesh( geometry, material );
mesh.position.set( 0, 0, 0 );
mesh.rotation.set( 0, - Math.PI / 2, 0 );
mesh.castShadow = true;
mesh.receiveShadow = true;
scene.add( mesh ); } ); }
function animate() {
requestAnimationFrame(animate);
renderer.render(scene, camera);
controls.update(); }
</script>
May take a little while to read the 3.7MB file. Please, be patient.
© 2011-2018, TecnoStats.