
Once you have opened a Maxima session, load package draw and then set global variable draw_renderer to vtk:
load("draw") $
draw_renderer: 'vtk $
In this section, we'll make extensive use of object triangle to build polyhedra. First, we define a set of vertices and write function make_triangles to plot sets of triangles.
/* Useful points */
vp:float(
[[0 ,0 ,2*%phi^2],
[%phi^2 ,0 ,%phi^3],
[%phi ,%phi^2 ,%phi^3],
[0 ,%phi ,%phi^3],
[-%phi ,%phi^2 ,%phi^3],
[-%phi^2 ,0 ,%phi^3],
[-%phi ,-%phi^2 ,%phi^3],
[0 ,-%phi ,%phi^3],
[%phi ,-%phi^2 ,%phi^3],
[%phi^3 ,%phi ,%phi^2],
[%phi^2 ,%phi^2 ,%phi^2],
[0 ,%phi^3 ,%phi^2],
[-%phi^2 ,%phi^2 ,%phi^2],
[-%phi^3 ,%phi ,%phi^2],
[-%phi^3 ,-%phi ,%phi^2],
[-%phi^2 ,-%phi^2 ,%phi^2],
[0 ,-%phi^3 ,%phi^2],
[%phi^2 ,-%phi^2 ,%phi^2],
[%phi^3 ,-%phi ,%phi^2],
[%phi^3 ,0 ,%phi],
[%phi^2 ,%phi^3 ,%phi],
[-%phi^2 ,%phi^3 ,%phi],
[-%phi^3 ,0 ,%phi],
[-%phi^2 ,-%phi^3 ,%phi],
[%phi^2 ,-%phi^3 ,%phi],
[2*%phi^2 ,0 ,0],
[%phi^3 ,%phi^2 ,0],
[%phi ,%phi^3 ,0],
[0 ,2*%phi^2 ,0],
[-%phi ,%phi^3 ,0],
[-%phi^3 ,%phi^2 ,0],
[-2*%phi^2 ,0 ,0],
[-%phi^3 ,-%phi^2 ,0],
[-%phi ,-%phi^3 ,0],
[0 ,-2*%phi^2 ,0],
[%phi ,-%phi^3 ,0],
[%phi^3 ,-%phi^2 ,0],
[%phi^3 ,0 ,-%phi],
[%phi^2 ,%phi^3 ,-%phi],
[-%phi^2 ,%phi^3 ,-%phi],
[-%phi^3 ,0 ,-%phi],
[-%phi^2 ,-%phi^3 ,-%phi],
[%phi^2 ,-%phi^3 ,-%phi],
[%phi^3 ,%phi ,-%phi^2],
[%phi^2 ,%phi^2 ,-%phi^2],
[0 ,%phi^3 ,-%phi^2],
[-%phi^2 ,%phi^2 ,-%phi^2],
[-%phi^3 ,%phi ,-%phi^2],
[-%phi^3 ,-%phi ,-%phi^2],
[-%phi^2 ,-%phi^2 ,-%phi^2],
[0 ,-%phi^3 ,-%phi^2],
[%phi^2 ,-%phi^2 ,-%phi^2],
[%phi^3 ,-%phi ,-%phi^2],
[%phi^2 ,0 ,-%phi^3],
[%phi ,%phi^2 ,-%phi^3],
[0 ,%phi ,-%phi^3],
[-%phi ,%phi^2 ,-%phi^3],
[-%phi^2 ,0 ,-%phi^3],
[-%phi ,-%phi^2 ,-%phi^3],
[0 ,-%phi ,-%phi^3],
[%phi ,-%phi^2 ,-%phi^3],
[0 ,0 ,-2*%phi^2]])$
/* faces are built with triangles */
make_triangles([v]) :=
map(lambda([z], triangle(vp[z[1]], vp[z[2]], vp[z[3]])),
v) $
/* Some draw defaults */
set_draw_defaults(
dimensions = [350, 350],
axis_3d = false )$
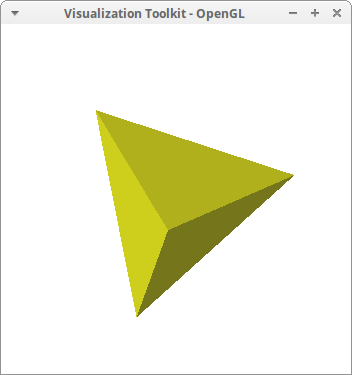
Tetrahedron:
draw3d(
color = yellow,
opacity = 2/3,
make_triangles([4, 34, 47],[4, 38, 34],
[4, 47, 38],[34, 38, 47])) $
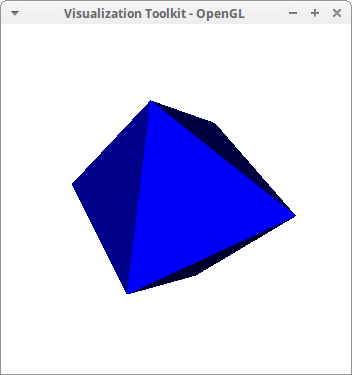
Cube:
draw3d(
color = blue,
background_color = green,
make_triangles([ 4, 18, 38], [38, 28, 4], [ 4, 23, 18], [18, 23, 34],
[ 4, 28, 47], [ 4, 47, 23], [28, 38, 60], [28, 60, 47],
[23, 47, 34], [47, 60, 34], [38, 18, 60], [18, 34, 60])) $

Octahedron:
draw3d(
make_triangles([ 7, 10, 43], [ 7, 22, 10], [ 7, 43, 49], [ 7, 49, 22],
[55, 10, 43], [55, 22, 10], [55, 43, 49], [55, 49, 22])) $
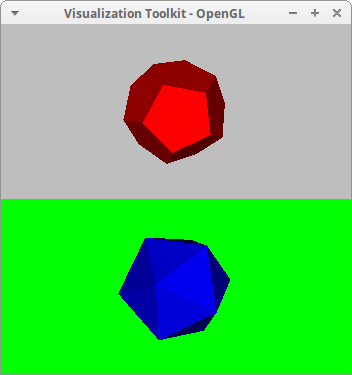
Dodecahedron and icosahedron:
draw(
columns = 1,
gr3d(
color = red,
axis_3d = false,
background_color = gray,
make_triangles([ 4, 8, 11], [11, 8, 18], [11, 18, 20],
[ 4, 13, 23], [ 4, 23, 8], [ 8, 23, 16],
[ 4, 11, 28], [ 4, 28, 30], [ 4, 30, 13],
[ 8, 16, 34], [ 8, 34, 18], [18, 34, 36],
[11, 20, 28], [20, 45, 28], [20, 38, 45],
[13, 30, 23], [23, 30, 41], [41, 30, 47],
[16, 23, 34], [34, 23, 50], [50, 23, 41],
[18, 36, 52], [18, 52, 38], [18, 38, 20],
[28, 45, 56], [28, 56, 47], [28, 47, 30],
[34, 50, 60], [34, 60, 36], [36, 60, 52],
[38, 52, 60], [38, 60, 56], [38, 56, 45],
[41, 47, 56], [41, 56, 60], [41, 60, 50] )),
gr3d(
color = blue,
axis_3d = false,
background_color = green,
make_triangles([ 2, 6, 17], [ 2, 12, 6], [ 2, 17, 37], [ 2, 37, 27],
[ 2, 27, 12], [37, 54, 27], [27, 54, 46], [27, 46, 12],
[12, 46, 31], [12, 31, 6], [ 6, 31, 33], [ 6, 33, 17],
[17, 33, 51], [17, 51, 37], [37, 51, 54], [58, 54, 51],
[58, 46, 54], [58, 31, 46], [58, 33, 31], [58, 51, 33] ))) $
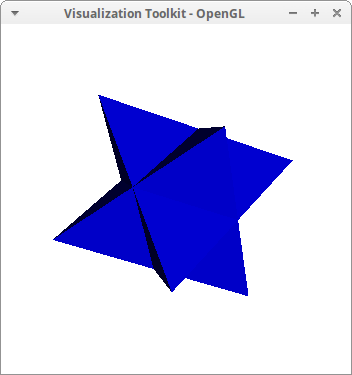
Intersecting tetrahedra:
draw3d( make_triangles([ 4, 34, 47],[4, 38, 34],[4, 47, 38],[34, 38, 47]), make_triangles([18, 23, 28], [18, 23, 60], [18, 28, 60], [23, 28, 60])) $
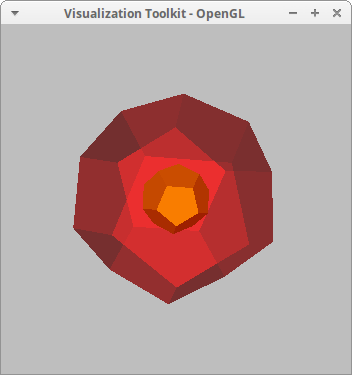
Playing with opacity and scaling:
dode: make_triangles([ 4, 8, 11], [11, 8, 18], [11, 18, 20],
[ 4, 13, 23], [ 4, 23, 8], [ 8, 23, 16],
[ 4, 11, 28], [ 4, 28, 30], [ 4, 30, 13],
[ 8, 16, 34], [ 8, 34, 18], [18, 34, 36],
[11, 20, 28], [20, 45, 28], [20, 38, 45],
[13, 30, 23], [23, 30, 41], [41, 30, 47],
[16, 23, 34], [34, 23, 50], [50, 23, 41],
[18, 36, 52], [18, 52, 38], [18, 38, 20],
[28, 45, 56], [28, 56, 47], [28, 47, 30],
[34, 50, 60], [34, 60, 36], [36, 60, 52],
[38, 52, 60], [38, 60, 56], [38, 56, 45],
[41, 47, 56], [41, 56, 60], [41, 60, 50] )$
draw3d(
background_color = gray,
opacity = 0.5,
color = red,
dode,
opacity = 1,
color = yellow,
transform = [x/3,y/3,z/3,x,y,z],
dode ) $
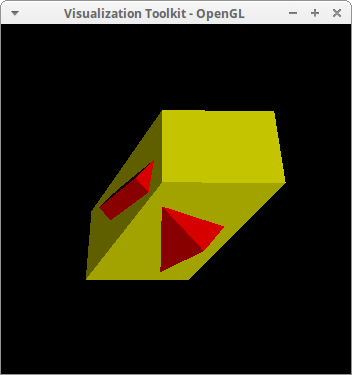
Linear transformation of a cube:
box: make_triangles([ 4, 18, 38], [38, 28, 4], [ 4, 23, 18], [18, 23, 34],
[ 4, 28, 47], [ 4, 47, 23], [28, 38, 60], [28, 60, 47],
[23, 47, 34], [47, 60, 34], [38, 18, 60], [18, 34, 60]) $
draw3d(
background_color = black,
color = red,
box,
color = yellow,
transform = [x+y,y+z,z+x,x,y,z],
box ) $
© 2016, TecnoStats.