Once you have opened a Maxima session, load package draw and then set global variable draw_renderer to vtk:
load("draw") $
draw_renderer: 'vtk $
A pyramid constructed by three triangles of different colors:
draw3d( color = blue, triangle([0,0,0], [2,0,0], [3,1,2]), color = yellow, triangle([0,0,0], [2,2,0], [3,1,2]), color = gray, triangle([2,0,0], [2,2,0], [3,1,2]) ) $
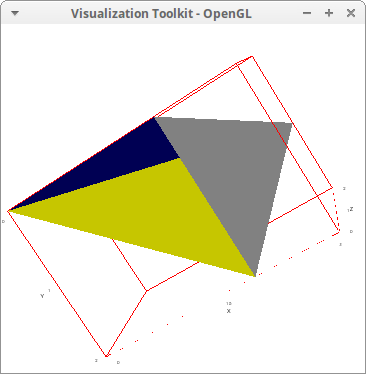
Quadrilateral as two adjacent triangles:
draw3d( triangle([0,0,2], [5,0,2], [2,3,2]), triangle([6,3,2], [5,0,2], [2,3,2]), color = red, triangle([0,0,5], [5,0,5], [2,3,5]), triangle([6,3,5], [5,0,5], [2,3,5]) ) $
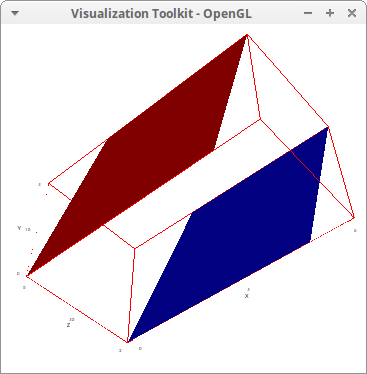
We now generalize some ideas used above in order to extend draw capabilities related to polygons. First, we need to know how to plot polyhedran angles:
/* v: the vertex of the polyhedran angle,
[p]: endpoints of the segments, all of them
starting at point v. */
polyhedral_angle(v, [p]) :=
block([np],
if listp(v) and length(v) = 3 and (np: length(p)) > 1
then makelist(triangle(v, p[k], p[k-1]), k, 2, np)
else funmake('polyhedral_angle,cons(v,p))) $
/* an example; note that point [1,2,3] is
repeated to close the polyhedran angle */
draw3d(
color = yellow,
polyhedral_angle(
[0,0,6], /* <-- the first point is the vertex */
[1,2,3], [2,2,-2], [4,-1,0], [2,-2,2],
[-1,-1,2],[-6,-2,3], [-8,5,5], [1,2,3]) )$
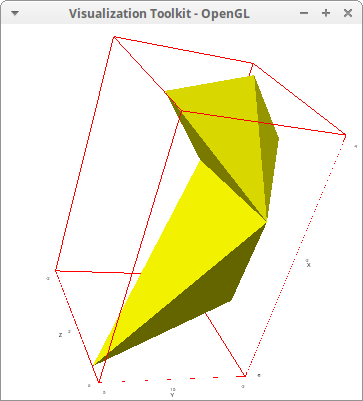
If all points are coplanar, we can plot arbitrary convex polygons. In this example, they all belong to the xy plane
draw3d(
color = yellow,
polyhedral_angle(
[0,0,0],
[1,2,0], [2,2,0], [4,-1,0], [2,-2,0],
[-1,-1,0],[-6,-2,0], [-8,5,0], [1,2,0]) )$
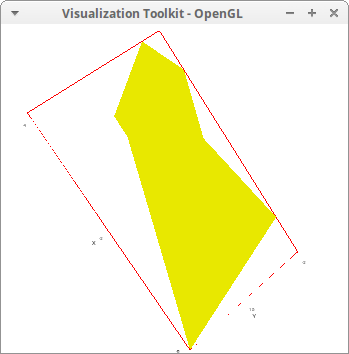
We can now draw regular polygons in all positions and orientations. Let's first define a function that returns a transformation matrix to rotate a point an angle th around a line passing through point poi and parallel to vector vec. After that, we define a function to calculate the vertices of a regular polygon
rotation3d(th,vec,poi) :=
block([c,s,t,u,v,w,a,b,d],
c : cos(th),
s : sin(th),
t : 1 - c,
[u,v,w] : vec / sqrt(apply("+", vec^2)),
[a,b,d] : poi,
matrix(
[u^2+(v^2+w^2)*c, t*u*v-s*w,
t*u*w+s*v, (a*(v^2+w^2)- u*(b*v+d*w))*t+(b*w-d*v)*s],
[t*u*v+s*w, v^2+(u^2+w^2)*c,
t*v*w-s*u, (b*(u^2+w^2)- v*(a*u+d*w))*t+(d*u-a*w)*s],
[t*u*w-s*v, t*v*w+s*u,
w^2+(u^2+v^2)*c, (d*(u^2+v^2)- w*(a*u+b*v))*t+(a*v-b*u)*s],
[0, 0, 0, 1] ))$
/* Generates the vertices of a regular polygon:
n: number of vertices
u: a vector orthogonal to the polygon
p: point origin of vector u
v: coordinates of one of the vertices of the regular polygon */
regular_polygon_vertices(n,u,p,v) :=
block([vs: [endcons(1,v)], m],
m: rotation3d(2*%pi / n, u, p),
for k:2 thru n do
vs: cons(first(transpose(m . first(vs))), vs) ,
map(lambda([z], [z[1], z[2], z[3]]), vs) )$
/* Here is an example; the coordinates of the penthagon centered at [4,-2,1],
with one vertex at [5,2,6/7], and orthogonal to vector [5,2,8] */
points: float(regular_polygon_vertices(5,[5,2,8],[4,-2,1],[5,2,6/7])) $
/* note that we make use of function polyhedral_angle,
where the vertex of the polyhedral angle is one of the vertices
of the polygon */
draw3d(
axis_3d = false,
color = gray,
apply(polyhedral_angle,points))$

Pressing the w key will show the wire structure of the polygon.
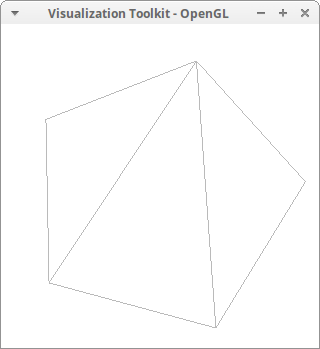
Geometric transformation of a triangle. The three vertices are transformed, and then a new triangle is drawn:
poly3: triangle([0,0,0], [2,0,0], [3,1,2]) $ draw3d( poly3, color = red, transform = [x+1,x*y^2,z+1,x,y,z], poly3 ) $
© 2016, TecnoStats.