'draw'-VTK interface:
object tube

Once you have opened a Maxima session, load package draw and then set global variable draw_renderer to vtk:

load("draw") $
draw_renderer: 'vtk $

To read the documentation on object tube, write the following sentence:

describe(tube) $

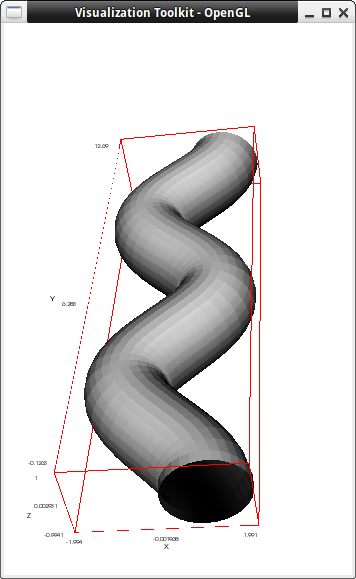
This is a simple tube. The three first arguments define a parametric curve, the fourth parameter is the radius of the tube as a function of the same parameter, whose name is declared in the fifth position, being the two last arguments its limits of variation. In this case, the radius is constant:

draw3d(
  enhanced3d = true,
  palette    = gray,
  xu_grid    = 50,
  tube(cos(a), a, 0, 1, a, 0, 4*%pi) )$

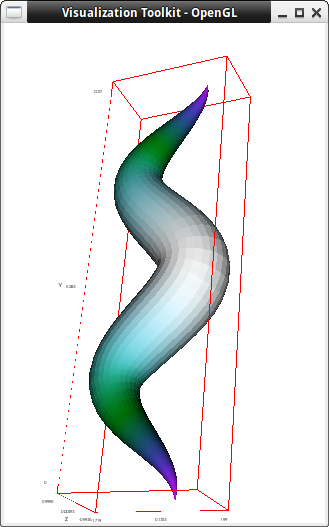
The same as before, but with varying radius. Color scalars are equal to the radius:

draw3d(
  enhanced3d = sin(a/4),
  palette    = [12,3,-14],
  xu_grid    = 50,
  tube(cos(a), a, 0, sin(a/4), a, 0, 4*%pi) )$

A family of knots:

knot(m,n,h,p,q,t,k,i,r,s) :=
  block([a],
        gr3d(xu_grid    = 100,
             enhanced3d = true,
             tube(m * cos(p*a) + n*cos(q*a) + k*cos(r*a),
                  m * sin(p*a) + n*sin(q*a) + k*sin(r*a),
                  h * sin(t*a) + i*sin(s*a),
                  0.1,
                  a, 0, 2*%pi)))$

k1 : knot(1,1.5,0.35,1,-2,3,0,0,0,0) $
k2 : knot(1,0.45,0.35,2,-3,5,0,0,0,0) $
k3 : knot(1,0.45,0.35,3,-2,5,0,0,0,0) $
k4 : knot(1,0.45,0.35,4,-1,5,0,0,0,0) $

draw(columns = 2, k1, k2, k3, k4 )$

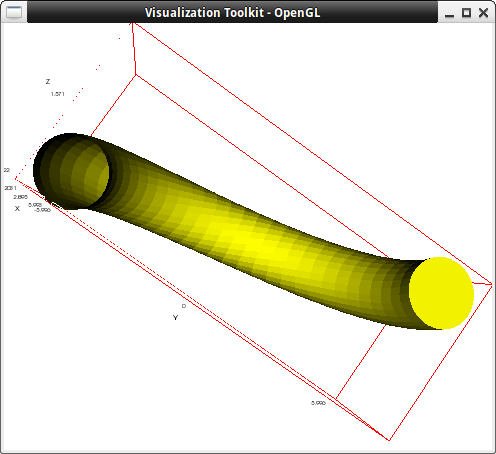
Tubes take into account the value of option capping:

draw3d(
  capping = [true, false],
  color   = yellow,
  tube(5*sin(t), 5*cos(t), t, 1, t, 0, %pi) )$

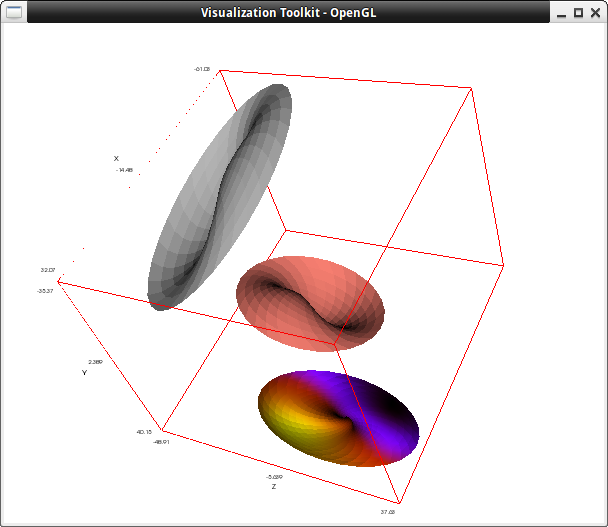
Three versions of the same tube. This example shows geometric transformations and the use of different palettes:

original: tube(t*cos(t),t*sin(t),t,exp(t)-1,t,0,%pi) $

draw3d(
    color      = salmon,
    original,

    enhanced3d = [x,x,y,z],
    transform  = [y+20,z-y+20,x+20,x,y,z],
    original,

    palette    = gray,
    transform  = [2*z-25,y-25,x-25,x,y,z],
    original )$

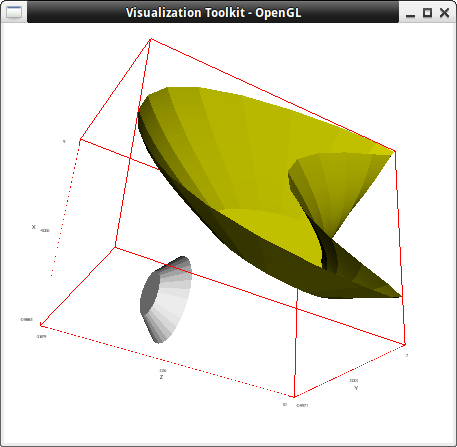
A truncated cone and a non linear transformation of it:

tcone: tube(1, 1, t, t, t, 1, 2) $

draw3d(
    capping = [true, false],
    color   = white,
    tcone,

    color     = yellow,
    transform = [x*2+3,5*z-3,7*sin(y)+3,x,y,z],
    tcone )$

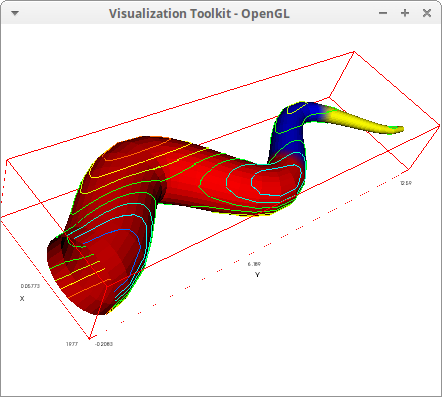
Isolines on a tube surface.

draw3d(
  enhanced3d = a^2,
  isolines   = [sin(x*z),x,y,z],
  palette    = [red, blue, yellow],
  line_width = 2,
  tube(cos(a), a, 0, cos(a/10)^2, a, 0, 4*%pi) )$

A mesh represented by tubes and exported to PLY format (this terminal will be available in Maxima 5.39). An idea from Eric Barth (thanks).

f(u,v):=u^2-v^2 $
r:.02$
tubesU: makelist( tube(x,i,f(x,i),r,x,-1,1),i,-1,1,.2) $
tubesV: makelist(tube(i,y,f(i,y),r,y,-1,1),i,-1,1,.2) $
corners: makelist(
            makelist(parametric_surface(i+r*cos(s)*cos(t),
                                        j+r*cos(s)*sin(t),
                                        f(i,j)+r*sin(s),
                                        s,0,2*%pi,t,0,%pi),
                     i,[-1,1] ),
            j,[-1,1]) $

draw3d(
    terminal  = ply,
    file_name = "mesh",
    xrange    = [-1-r,1+r],
    yrange    = [-1-r,1+r],
    tubesU, tubesV, corners)$

Drag the mouse on the picture.

'draw'-VTK interface:object tube

'draw'-VTK interface:
object tube