Back to main page
Back to sound contents

This section shows some uses of the Discrete Fourier Transform applied to waveforms. First thing to do is to load Maxima's fft package:

load("fft") $

Since we want to play the sound and draw the waveform everytime we call the play function, we set some sound options defaults to avoid rewriting them.

set_sound_defaults(
   player    = "mplayer",
   normalize = none,
   draw_wave = true,
   draw_wave_options = [dimensions = [800, 600]] )$

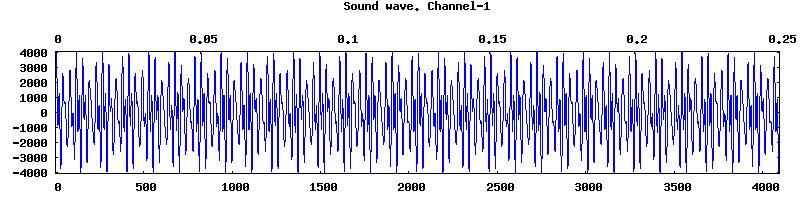
Let's sum three sinusoidal waves of different frequency and amplitude.

play(
  wave(2000*sin(2*%pi*440*t), t, 0, 0.25),
  wave(1500*sin(2*%pi*880*t), t, 0, 0.25),
  wave(1000*sin(2*%pi*1000*t), t, 0, 0.25)) $

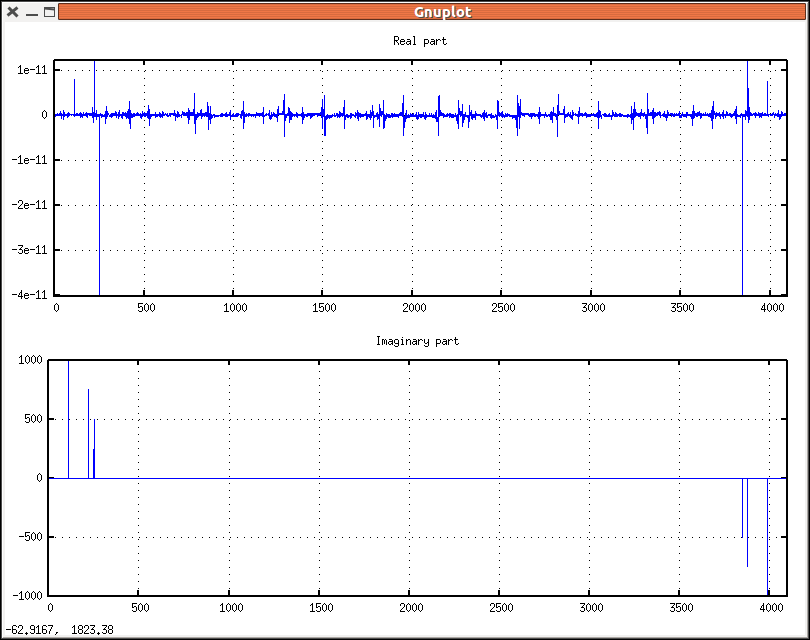
Now, let's calculate the DFT of this waveform:

/* Create the real and imaginary arrays */
/* Number 1 stands for channel 1 */
tf: fft(sound_sample_list(1)) $

/* extract real and imaginary components */
rtf: realpart(tf) $
itf: imagpart(tf) $

/* Let's draw the DFT */
set_draw_defaults(
   dimensions  = [800, 600],
   points_joined = true,
   point_type    = dot,
   grid          = true) $

draw(
   gr2d(
      title = "Real part",
      points(rtf)),
   gr2d(
      title = "Imaginary part",
      points(itf))) $

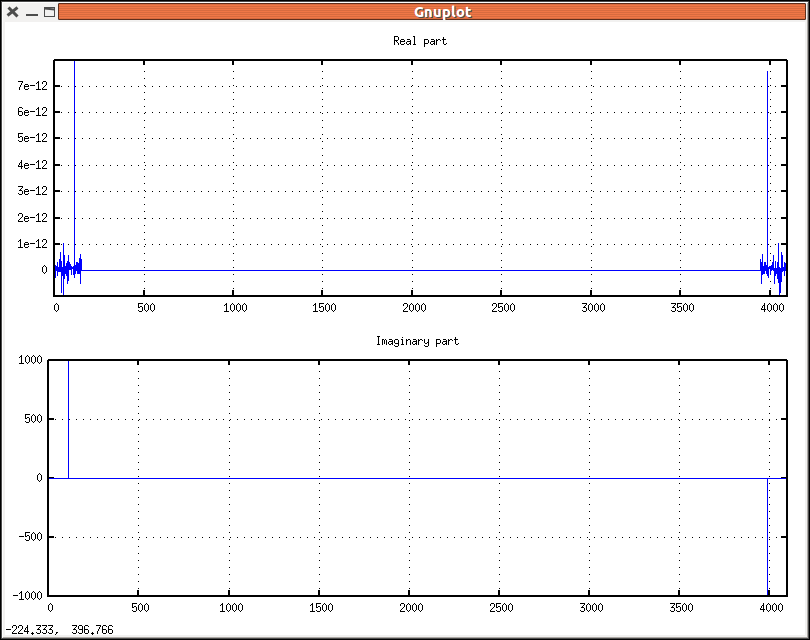
We plan to remove the components with frequencies 880 and 1000 Hz, setting to zero the elements of real_dft_array and imag_dft_array in the range 150 thru 3946 = array_length(sound_sample)-150.

for i: 150 thru 3946 do (
   rtf[i] : 0.0,
   itf[i] : 0.0 ) $

draw(
   gr2d(
      title = "Real part",
      points(rtf)),
   gr2d(
      title = "Imaginary part",
      points(itf))) $

Now it's time to calculate de Inverse Discrete Fourier Transform (IDFT) to get the filtered wave. As is visible and audible, the signal is a A4 (Do4) note.

invtf: inverse_fft(rtf + itf*%i) $
play(sample(realpart(invtf))) $

Back to main page
Back to sound contents